Совершенствование управления любой организацией связано с автоматизацией бизнес процессов планирования и отчетности, внедрением бюджетирования. На опыте работ с МПС и разработки системы планирования показателей деятельности Куйбышевской железной дороги получено программное решение, позволяющее оптимизировать и ускорить бизнес процессы планирования и отчетности. Это достигается за счет возможности коллективной и одновременной работы над планами и отчетами разной степени агрегации. Новизна предлагаемого в данной статье подхода состоит в использовании сводного отчета для динамической модификации данных и навигации для построения формул.
Вполне естественно и оправданно желание пользователей различных OLAP средств редактировать суммарные значения в ячейках отчета, например сводный отчет в Excel или многомерный отчет SAS/EIS, однако, сейчас это невозможно и данные можно только просматривать. Потребности в редактировании касаются не только планируемых величин, но и отчетных данных, ведь принципиальной особенностью автоматизируемых бизнес процессов является замена отсутствующих на момент планирования отчетных данных их оценочными значениями. Разработка решения на основе редактируемой многомерной базы данных, позволит расширить нишу класса программных продуктов, основанных на интерактивном построении и модификации многомерных структур данных. Ведь на рынке присутствует много программных продуктов по планированию, которые не позволяют произвольно изменять данные, например, нельзя изменять длительности в Microsoft Project сверху вниз.
Вычислительная целостность агрегатов данных является главным препятствием для произвольного изменения данных многомерной структуры, поэтому сосредоточимся на изменениях данных, сохраняющих вычислительную целостность. Многомерная структура данных (далее MDDS) представляет собой таблицу из набора агрегатных таблиц (подпространств), полученных свертками детальной таблицы (пространства) по комбинациям измерений. Процедуры SAS PROC SUMMARY или PROC MEANS умеют создавать такую структуру.
В процессе совместных работ специалистов по информатизации компании IBS с экономистами МПС, мы встретились с тремя основными проблемами:
- Как удобным образом управлять описаниями и данными показателей, характеризующими работу железной дороги или всей отрасли, когда их число составляет от нескольких сотен до тысяч, и они в сводном виде представлены на бумажных носителях в виде набора таблиц — форм отраслевой отчетности, числом от нескольких десятков до сотен?
- Как формировать вычисления производных показателей таким образом, чтобы экономисты сами могли задавать вычислительные модели и формировать методики расчетов?
- Как редактировать многомерную структуру, сохраняя вычислительную целостность, без представления базы данных в виде множества отдельных таблиц связанных ссылками (нормализации базы по ER модели сущность-связь), во избежание неэффективных операций по денормализации базы данных?
Нас в первую очередь интересовали вопросы о соотношении подходов по многомерному моделированию данных с ER моделированием и о том, как эти подходы переходят друг в друга. Ключевые моменты:
- в отличие от многомерной базы, нормализованная ER модель слишком узко ориентирована, на ввод данных, на работу с фиксированным набором иерархий, а добавление новой иерархии затруднительно;
- практически любая таблица из альбома форм отраслевой отчетности является каким-то срезом гипотетической многомерной базы данных;
- все многообразие отчетов по многомерной базе данных является различными представлениями одного геометрического объекта в разных координатах;
- оптимизация физической структуры многомерной базы данных основана на выборе конкретного оптимального варианта базы из множества эквивалентных представлений базы как геометрического объекта;
- все три упомянутые проблемы имеют общий фундамент — управление большим количеством объектов и описание решения посредством комбинаций относительно небольшого количества параметров (оси многомерного пространства и значения измерений на них);
- по всей видимости, для описания упомянутых проблем наиболее подходит аппарат тензорного исчисления. Он включает операции свертки-развертки по измерениям и формулы пересчета компонентов при изменении системы координат и преобразования пространства, допускает формулировку финансово-экономической модели развития предприятия, конечно, на основе законов сохранения.
Правда, пока нет каких-либо примеров применения аппарата тензорного исчисления к финансово-экономическим расчетам с использованием технологии OLAP, возможно, это дело будущего.
Наша работа была посвящена разбору структуры и обоснованию редактирования многомерной базы с сохранением вычислительной целостности для операции суммирования. Другие статистики, например, среднее значение, пока не рассматривались, хотя к ним применим несколько более сложный подход. После предварительного рассмотрения декомпозиции многомерной структуры, даются ответы на следующие вопросы:
- Что означает редактирование значения статистики в любой агрегатной точке?
- Какие изменения следует произвести для сохранения вычислительной целостности многомерной структуры данных?
- Как управлять верхней границей консолидации, предохраняющей от изменения данные, лежащие выше определенного уровня агрегации?
Возможности ручного редактирования усиливаются при использовании формул и при загрузке данных или значений измерений из файлов, например, таблиц Еxcel.
Автоматизация бизнес процессов
Планирование — это сложный итерационный процесс, включающий элементы переговоров, в которых задействовано много людей из различных уровней организационной структуры. Бизнес процесс сбора отчетов состоит в консолидации фактических данных по истекшим интервалам времени и оценочных данных по не истекшим еще интервалам. Эти два бизнес процесса близко связаны, поскольку принятие управленческих решений основано на сопоставлении показателей плана и факта, для чего они описываются в одних измерениях и в одних значениях измерений. Несмотря на то что за каждый бизнес процесс отвечают различные подразделения организации, и планы не детализируются так глубоко как факты, для целей автоматизации, планы и отчеты удобно поддерживать на основе общей базы данных.
Исходим из того, что для автоматизации бизнес процессов планирования и сбора отчетов, следует сосредоточиться на порождаемых этими бизнес процессами преобразованиях данных и построить их математическую модель. Чем лучше модель отразит реальные черты трансформации данных, тем легче и дешевле провести автоматизацию. Слабая модель может не препятствовать автоматизации, однако, приведет к излишним и прогрессирующим затратам ресурсов при продвижении по стадиям жизненного цикла программного продукта.
Предполагаем, что бизнес процесс планирования ресурса порождает преобразования данных со следующими двумя характерными особенностями:
- перераспределение значений ресурса с уровней высокой агрегации на уровни низкой агрегации;
- перераспределение значений по горизонтали в пределах одного уровня агрегации из одних ячеек в другие.
Бизнес процесс сбора отчетов порождает преобразования в противоположном направлении — консолидацию детальных данных в агрегированные. Обычна ситуация, когда плановик работает с отчетом из середины структуры и имеет дело со смесью этих двух типов преобразований данных, направленных в противоположных направлениях. С одной стороны плановик получает сверху лимиты на ресурсы и распределяет их более детально на нижние уровни агрегации, которые становятся лимитами для плановиков следующего нижнего уровня. С другой стороны, детальные значения консолидируются в агрегатные значения, которые представляются для просмотра и анализа плановиками верхнего уровня.
Свойства многомерной структуры
Из системы определений многомерной модели вытекают многочисленные свойства структуры.
Декомпозиция MDDS на параллелотопы
Параллелотоп состоит из детальной точки и получаемых из нее всеми свертками агрегатных точек. Все параллелотопы имеют общую точку — начало координат, и могут пересекаться в других агрегатных точках. Значение меры в агрегатной точке равно сумме мер всех параллелотопов, пересекающих точку. Таким простым образом, посредством композиции геометрических фигур, объясняется сложное представление многих иерархий агрегатов, которые можно пытаться строить на детальных точках.
 |
| Рис. 1. Декомпозиция MDDSДекомпозиция MDDS из трех детальных точек (1,2,3) для двух измерений (D1, D2). Три прямоугольника (параллелотопа) задаются детальными точками, а в шести других точках мы наблюдаем суперпозицию (пересечение) прямоугольников, 2+3 обозначает суммирование мер 2 и 3 прямоугольника. |
В случае двух измерений мы имеем набор частично пересекающихся прямоугольников, задаваемых детальными точками (рис. 1), для случая трех измерений имеем набор параллелепипедов и т.д.
Общий вид MDDS
Рассмотрим пример MDDS для случая трех измерений «Квартал», «Месяц», «Завод» с декомпозицией показателя «Доход» на параллелотопы как показано на рис. 2, что позволяет проводить конкретное обсуждение, впрочем, без ограничения общности.
Иерархии агрегатов
В структуре MDDS значения «Тип» показывают номер агрегатного подпространства в двоичном представлении, где 0 в какой-то позиции обозначает произведенную свертку по соответствующему измерению, а 1 обозначает, что свертки нет, данные развернуты. Детальная таблица определяется значением «Тип» равной строке из единиц, т.е. данные развернуты по всем измерениям. Максимально возможное число агрегатов равно 2N.
Количество возможных путей свертки детальной таблицы в точку — начало координат равно N!, и обратно столько же способов развертки нулевого агрегата в детальную таблицу. Тип агрегата при свертке вдоль измерения изменяется заменой 1 на 0 в позиции, соответствующей этому измерению. Поскольку последовательность развертки задается порядком следования измерений, по которым она происходит, то отношение N!/2N является грубой оценкой количества иерархий, в которых может участвовать одна агрегатная таблица, это отношение много больше 1 уже при N>4.
Таким образом, в структуре MDDS присутствуют иерархии агрегатных таблиц, т.е. наборы последовательной из N таблиц, в типе последовательно добавляется по 1. Эти наборы таблиц содержат предварительно вычисленные значения статистик и используются для быстрой навигации по данным.
Иерархия геометрических объектов
Столбец «Доход» в детальной таблице представляет геометрическую фигуру, которая управляется группой перестановок измерений и значений измерений. Столбцы F0-F7 в детальной таблице дают наглядное представление о группе перестановок по перемещению точек со значениями F0-F7 при перестановке измерений или значений измерений.
Термин детальная таблица или агрегатная таблица условен — каждая агрегатная таблица может рассматриваться как детальная в подпространстве своих развернутых измерений, и ее геометрическая фигура является результатом свертки фигуры всего детального пространства. Таким образом, мы имеем согласованную в вычислительном смысле иерархию геометрических фигур, которая управляется группой перестановок измерений и их значений как одна цельная геометрическая фигура.
Развертка в разных направлениях
Одна из главных особенностей MDDS — возможность разворачивать любое агрегатное значение в различных направлениях, можно также использовать комбинаторные наборы направлений. Чем глубже мы находимся в MDDS, тем меньше остается возможных направлений раскрытия. Но в каждую точку мы можем придти из N направлений для N-мерного пространства.
Минимальным по сложности структурным элементом развертки является комбинация отрезков мастер-деталь, где мастер отрезок с агрегатными точками, деталь перпендикулярный отрезок, пробегающий концом по этим точкам. Возможность развертки по одному измерению и сразу по двум показаны на рис. 4.
 |
| Рис. 4. Развертка агрегатных значений Последовательная развертка агрегатных значений отрезками (слева) или плоскостями (справа) мастер-деталь. Значение в общей точке мастер-деталь равна сумме значений в остальных точках детали. |
В общем случае, если агрегатная точка задает гиперплоскость размерности M в пространстве размерности N, то она является общей точкой мастер подпространства размерности N-M и детального подпространства размерности M (гиперплоскости). Если из М измерений детального пространства сделать два составных, то их пересечение дает двухмерный отчет, где агрегатная точка — сумма по столбцам, равная сумме по строкам.
Структура бизнес измерений
Если многомерное пространство строится путем добавления измерений из всех подряд относящихся к задаче дискретных показателей, то его объем быстро превышает объем данных любой реальной задачи, поскольку значения измерений связаны зависимостями и большая часть точек в пространстве оказываются пустыми. При статистической обработке таких данных сначала выделяют информативное подпространство методами многомерного анализа, т.е. пространство независимых измерений.
При проектировании предметно-ориентированных информационных систем на базе OLAP такое информативное подпространство обычно считается заранее известным по характеру предметной области, его образуют бизнес измерения, (фактически независимые). Обычный подход проектирования состоит в создании бизнес измерений и значений на осях, соответствующим всем узлам иерархии, например, годы, кварталы, месяцы для оси времени или статьи и подстатьи бюджета для оси бюджета. Заполнение значениями производится вручную или загрузкой из файлов. Затем задаются формулы вычислений значений в одних точках по другим (модель). Последующее функционирование системы основано на работе с многомерным массивом, значения измерений которого образованы точками бизнес измерений.
Этот подход применяется, например, в продуктах Oracle Financials, SAS/CFO Vision. Однако используемые бизнес измерения являются только подмножеством всех возможных составных измерений, образуемых комбинациями простых, имеется много других составных и простых измерений, осмысленных с точки зрения предметной области. Важно, однако, что этот подход укладывается в рамки более общей картины эквивалентных представлений MDDS.
Эквивалентные представления MDDS
Существует множество эквивалентных представлений MDDS в пространствах размерности 1, 2, …, N, где N — число простых измерений, и есть правила преобразований из одного представления в другое. Это напоминает разнообразие представлений чисел в разных системах счисления и правил перехода между ними, более того, оба явления имеют одну основу.
Разбивая множество простых измерений на 1, 2, ..., N непересекающихся групп, каждая из которых образует составное измерение, получаем отображение всех точек в пространство соответствующего числа составных измерений. При этом значения составного измерения также составляются из значений простых измерений. При разбиениях на две группы получаем представление MDDS на плоскости c шапкой и боковиком иерархической структуры (рис. 3).
При последовательном переходе от одномерного пространства к двух, трех и ... N — мерному происходит добавление пустых ячеек, в которых функция не определена, но они требуются для регулярности структуры (рис.3). Одномерное представление совсем не содержит пустых ячеек, но с каждой ячейкой необходимо хранить ее координаты в виде значений измерений (или их коды). А N-мерное пространство содержит максимальное количество пустых ячеек, но координаты хранить совсем не нужно, нужная ячейка находится как элемент многомерного массива по индексам — значениям простых измерений.
Таким образом, имеется два противоположных фактора затрат ресурсов по памяти на множестве эквивалентных представлений MDDS — хранение пустых ячеек и хранение координат. Соответствующую точку оптимальности можно учитывать при проектировании базы и работы с ней. Эквивалентные представления MDDS как пересечения измерений имеют практический смысл по следующим причинам:
- более компактно и информативно для обозрения;
- можно применить вычислительную модель над столбцами, поскольку модель вычислений над строками обычно не предусмотрена;
- одно, два и более мерные представления полезны для поиска оптимальной физической структуры базы данных;
- формализация управления показателями при помощи составных имен.
Редактирование многомерной структуры
Под редактированием MDDS будем понимать такие изменения значений функции в многомерном пространстве и ее области определения посредством добавления или удаления детальных точек, агрегатных точек, измерений, которые сохраняют вычислительную целостность структуры.
Из свойства декомпозиции MDDS на параллелотопы редактирование обеспечивается добавлением в структуру (удалением, изменением) некоторых параллелотопов. Для детальной точки это очевидно, потому что только один параллелотоп всегда проходит через каждую детальную точку (задается ей). Следует различать редактирование как измерение значения в точке и создание самой точки с нулевым значением, что является формированием структуры связей между значениями показателей, схемы базы.
Изменение значения в агрегатной точке
Мера в агрегатной точке равна сумме мер параллелотопов, пересекающих эту точку, поэтому для изменения значения в агрегатной точке при сохранении вычислительной целостности необходимо и достаточно добавить (вычесть) в многомерную структуру параллелотоп, пересекающий эту агрегатную точку. Для конкретной агрегатной точки необходимо решить, какой параллелотоп из многих возможных следует добавить. Хотя бы одна детальная точка для него должна существовать, также можно использовать резервную точку, если неизвестно какую детальную точку следует использовать. Какая резервная точка должна быть использована? Для каждой агрегатной точки всегда существует единственная детальная резервная точка, которая определяется по правилу: все нулевые значения координат агрегатной точки заменяются значением РЕЗЕРВ. Параллелотоп полученной детальной точки гарантированно проходит через данную агрегатную точку и приносит в нее необходимое приращение значения.
Затем определяются все другие точки параллелотопа и модифицируется MDDS. На практике для поддержки иерархий используется ограниченное число агрегатных таблиц и не все вершины параллелотопа следует использовать, потому что каждая вершина соответствует одной агрегатной таблице. В самом простом случае достаточно хранить только детальную таблицу и вычислять все агрегаты «на лету», при этом все правила редактирования сохраняются.
Удаление агрегатной точки
Операция удаления агрегатной точки сложнее, чем добавление, и может повлечь удаление других точек. Сначала ее следует обнулить, что приводит к переносу ресурса в резервную точку согласно направлениям планирования. На втором шаге удаляется гиперплоскость, проходящая через данную агрегатную точку. Однако некоторые параллелотопы, основанные на удаляемых детальных точках, могут пересекать другие агрегатные точки с нулевыми значениями после удаления параллелотопа. Некоторые из этих агрегатных точек должны быть удалены, поскольку у них нет больше детальной точки, на которой основана их не пустота. Имеем некоторый аналог висячей ссылки при нарушении ссылочной целостности.
Эта проблема имеет следующее решение: если значение статистики N (число параллелотопов пересекающих точку) равно или меньше нуля после удаления всех детальных точек гиперплоскости, тогда эта агрегатная точка должна быть удалена.
Направления планирования и верхняя граница консолидации
При перераспределении резервного значения в агрегатную точку одного уровня происходит вычитание параллелотопа, проходящего через резервную точку и добавление параллелотопа, который проходит через целевую точку. Оба несут равные значения на своих вершинах. Создается эффект перераспределения значения из одной точки в другую на плоскости и пользователю нет необходимости понимать, что он видит только плоское представление результата многомерного процесса. Однако значение ресурса можно брать непосредственно с верхних уровней резерва текущего подпространства, в которое мы погрузились, настройкой направлений планирования для указания источника ресурса — резервной ячейки. Когда направления выключены, то добавляется только один параллелотоп, и модифицируются все агрегаты до самого верха.
Описанная суперпозиция производит практически полезный эффект верхней границы консолидации. На всех уровнях от уровня целевой ячейки до уровня резервной ячейки имеет место процесс консолидации, а выше резервной ячейки значения остаются неизменными, поскольку результат суперпозиции равен нулю. На рис. 4 показан эффект верхней границы консолидации для случая представления агрегатов трех уровней агрегатов на плоскости.
Модификация структуры базы
Приложение поддерживает возможность редактирования структуры MDDS самим пользователем, начиная с одной ячейки. По правой кнопке мыши из всплывающего меню выбирается команда «Изменить боковик». По положению активной ячейки определяется измерение, его значения представляются в окне «Модификация боковика», где производится выбор для добавления или удаления значений. Модификация шапки производится переносом измерения мышью в боковик, редактированием и обратным переносом.
Вычислительная модель
Вычислительная модель является необходимым средством при планировании, которое производится по специально разработанным экспертами-экономистами методикам. Вычислительная модель SAS/EIS ограничена простым измерением. Мы расширили ее для составного измерения, для построения формул из произвольных столбцов или строк и записи результатов в базу. Формула в ячейке может копироваться по нескольким измерениям, аргументы формулы могут иметь фиксированные значения по некоторым координатам. Когда пользователь строит формулу он использует многомерный отчет как навигатор по данным для нахождения нужных ячеек и выбирает их с помощью мыши. Управляющие элементы направлений планирования задают направления копирования формулы и абсолютные значения координат ячеек аргументов.
Общая архитектура решения
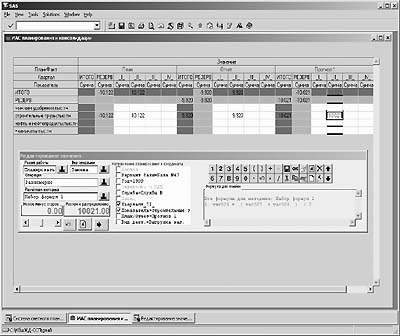 |
| Рис. 5. Основной интерфейс системы |
Результатом изложенных рассуждений стала архитектура системы для работы с системой согласованных отчетов (рис. 5). Многочисленные рабочие места для просмотра и редактирования планов и отчетов с табличной формируются настройкой шаблона многомерного отчета (рис. 6). На первый план технологии работы с общей базой отчетов выступает принцип вычислительной целостности, на нем основаны все модификации базы. Извлекаемые из базы и представляемые разным способом для разных клиентских мест отчеты остаются внутренне сбалансированными в процессе автономной работы и в результате запросов на обновления базы.
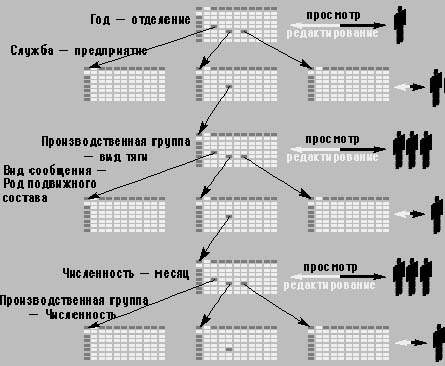 |
| Рис. 6. Совместная работа многих пользователей над системой всегда согласованных отчетов Иерархии задаются бизнес процессами и отражают вертикальные и горизонтальные отношения в структуре организации между пользователями. Соседние по вертикали отчеты имеют общие агрегатные ячейку, или строку или столбец. В светлых полях указана неувязка между отчетами. |
Все различия между отчетами разных уровней агрегации представляются в каждом отчете в его полях резерва. Положительные значения резерва означают лимиты ресурсов для детального распределения, отрицательные — заявку на ресурсы, а малые или нулевые значения в полях резерва свидетельствуют о согласованности планов. Плановики могут самостоятельно оценивать важность рассогласований, не дожидаясь сбора всех данных и вовремя концентрируясь на важных моментах планирования.
Выводы
Предложено основанное на новой математической модели программное решение, которое позволяет оптимизировать и ускорить бизнес процессы планирования и отчетности. Модель поддерживает редактирование многомерной структуры данных с сохранением вычислительной целостности. Проверка проведена на системе, реализованной на базе объекта SAS/EIS «Многомерный отчет» и путем программирования в SAS/AF.
Разобрано строение многомерной структуры, показана эквивалентность различных ее представлений в пространствах одного, двух и более измерений. Показано, что основная математическая функциональность объекта SAS/EIS «Многомерный отчет», реализует получение элементов многообразия представлений одной и той же геометрической фигуры, производимой группой перестановок измерений и значений измерений.
Геометрическая фигура (схема) образована набором всех не пустых детальных точек, в которых задается некоторая скалярная функция и агрегатных точек, в которых вычисляются значения функции. Если способ вычисления не зависит от пути свертки, например, суммирование, то функция допускает декомпозицию на элементарные геометрические фигуры — параллелотопы c постоянным значением функции на вершинах. Эти параллелотопы инвариантны относительно иерархий и являются минимальными элементами модификации многомерной структуры данных. Мы рассматриваем, что MDDS изменяется в приращениях от одного состояния к другому, при сохранении вычислительной целостности агрегатных сумм.
Введение уровней РЕЗЕРВ в значения измерений позволяет представить MDDS как набор согласованных иерархических отчетов с хранением невязки между ними в пространстве резерва. Уровни резерва обеспечивают необходимые степени свободы для редактирования значений в агрегатных точках и распределения данных в любом направлении как сверху вниз, так и по горизонтали на одном уровне агрегации. Структура MDDS хорошо приспособлена для назначения прав доступа и разграничения областей ответственности пользователей, это достигается введением дополнительного измерения. Любой многомерный отчет может быть использован как интерфейс для редактирования лежащей за ним многомерной структуры MDDS. Это в значительной степени отвечает практическим требованиям при поддержке бизнес процессов планирования ресурсов и консолидации отчетов, бюджетирования, и даже при распределении данных по бухгалтерским счетам.
В результате работы сформировалось общее видение архитектуры такой системы планирования и отчетности, которая предоставляет возможность независимой и совместной работы многих экономистов над своими планами и отчетами как частью всегда сбалансированных данных. Значения резерва (невязки) в каждом отчете выполняют коммуникативную роль, в разные моменты их можно игнорировать или наоборот учитывать. Экономистам больше не нужно ожидать момента полного сбора данных, они свободны в собственных оценках важности существующей невязки, что позволяет существенно сократить сроки подготовки планов.
Автор благодарен за оценку важности работы и поддержку при выполнении: Юрию Анатольевичу Полянскому, главному экономисту Куйбышевской ж.д. МПС РФ, за обсуждения и поддержку в программировании: Сергею Заблодскому (IBS), Рустему Файзуллину (Luxoft).
Евгений Гришенков (EGrishenkoff@ ibs.ru) — сотрудник компании IBS (г.Москва)
Статья была представлена на 26-й всемирной конференции пользователей системы SAS, SUGI26, SAS USERS GROUP INTERNATIONAL, 22-25, APRIL, 2001, LONG BEACH, CA, USA.
Система определений многомерной структуры данных MDDS
Для определенности вводим систему определений. По-видимому, общепринятой математической модели MDDS не существует, но мы пользовались наблюдениями функционирования объекта SAS/EIS «Многомерный отчет» и OLAP объектов других поставщиков программного обеспечения (SAP, Oracle, Microsoft, Cognos, Business Objects). Будем использовать как синонимы слова: точка многомерного пространства, узел многомерной решетки, элемент многомерной матрицы, ячейка многомерного отчета.
Измерение — ось с именованными точками (значениями измерений). Порядок точек и расстояния между ними не важны. Среди точек имеется нулевая точка и точка РЕЗЕРВ.
Многомерное пространство (решетка) — Декартово произведение измерений, пересекающихся в нулевых точках.
Событие — регистрация значения скалярной функции в точке многомерного пространства. Каждая запись события должна содержать набор атрибутов — значений измерений. Информационные системы, работающие на уровне детализации с событиями, называются системы регистрации фактов хозяйственной деятельности (транзакционные системы), а системы для отчетов, анализа и планирования работают со статистиками данных на интервалах времени.
Мера — скалярная функция, вычисляемая в точках пространства согласно определенным правилам. Мера типа 1 для детальной точки задается как суммарное значение по временному интервалу, для агрегатной точки вычисляется по всем детальным точкам, принадлежащим данной агрегатной точке. Мера типа 2 вычисляется по точкам одного уровня агрегации. Примерами меры типа 1 являются частота (N), сумма (SUM) и другие статистики в точке, для меры типа 2 — накопленные суммы за временной интервал.
Проективная гиперплоскость — это гиперплоскость, содержащая все узлы многомерной решетки с фиксированным значением одной или нескольких координат.
Детальная точка — такая точка многомерного пространства, у которой нет ни одной координаты со значением 0.
Агрегатная точка — точка многомерного пространства, в координатах которой присутствует хотя бы одно нулевое значение.
Резервная точка — точка многомерного пространства, в координатах которой присутствует хотя бы одно значение РЕЗЕРВ. Резервная точка может быть детальной или агрегатной.
Операция проектирования задает правила для вычисления меры типа 1 в узлах решетки следующим образом: мера в текущем узле вычисляется по всем узлам проективной гиперплоскости пересекающей текущий узел. Эта операция называется сверткой, а противоположная операция (при навигации по данным) — развертка.
Составное измерение — ось с именованными точками взаимно однозначно соответствующим всем непустым точкам подпространства, образованного некоторым набором измерений. Порядок точек и порядок измерений не важен.
Иерархия является составным измерением с наложенным порядком следования простых измерений. Она может быть представлена в виде графа из деревьев фиксированной высоты; число деревьев равно числу значений первого простого измерения, число уровней равно числу измерений. Порядок точек в любом измерении не важен, но перестановка точек приводит к перестановке соответствующих нижележащих поддеревьев.
Пересечение измерений — представление на плоскости Декартового произведения осей простых составных измерений, иерархий, когда в ячейках представлены значения меры.
Параллелотоп — геометрическая фигура (набор точек), получаемая всеми возможными операциями свертки детальной точки, значение меры в точках постоянно.
