Качество произведенного программного продукта, как и для всякого производства, является важным технологическим понятием: достижение приемлемого качества должно планироваться, а в процессе технологического цикла разработки качество должно быть предметом инспекций и контроля.
Классически исходное представление о качестве связано с тем, что разработанный продукт подтверждает свою спецификацию, при этом спецификация должна быть ориентирована на характеристики, которые желает получить клиент [1]. В работе [2] отмечается, что иная, не менее, широкая трактовка понятия качества может быть выражена утверждением "пригодность для цели". Так или иначе, понятие качества программного обеспечения - это прежде всего внешняя оценка. Степень качества связана с удовлетворением потребностей пользователя.
Современные технологические стандарты и учебники по технологии программирования уточняют понятие качества, вводя совокупность аспектов, в свете которых и должно рассматриваться качество. В работе [3], например, в роли таких аспектов выступают: безопасность, защищенность, надежность, устойчивость, понимаемость, тестируемость, адаптируемость, модульность, сложность, переносимость, доступность пользователю, повторная используемость, эффективность, изучаемость и сопровождаемость. Этот список достаточно полон и, по-видимому, включает все интересные для рассмотрения аспекты качества. Похожий перечень приводится и в монографии российского автора [4], однако с учетом того, что за десяток лет, разделяющий эти работы, понятие качества программного обеспечения претерпело определенную эволюцию.
С другой стороны, все или по крайней мере большинство из перечисленных аспектов качества определенным образом связано с некоторыми свойствами компонентов программной системы, а также со свойствами структуры программного обеспечения как системы компонентов. Негласно существует программистский "гамбургский счет" оценки качества программной реализации. Кстати, знакомство с исходными текстами ряда весьма уважаемых и широко используемых программных продуктов показывает, что по этому "гамбургскому счету" они выглядят не очень хорошо.
Действительно, разумная организация потока управления и информационных потоков в реализованной программе заведомо улучшает такие аспекты, как устойчивость, понимаемость, тестируемость, адаптируемость, переносимость, повторная используемость, сопровождаемость, да, возможно, и другие.
Для оценки внутренних достоинств реализации программы с технической стороны в работе [5] было предложено понятие добротности программы (в английском переводе [6] приведен соответствующий англоязычный термин "soundness"). В термин "добротность" вкладывается такой аспект хорошей программы, который заключается в том, что программа разумно, рационально реализована, с достаточно продуманной организацией потоков управления и информационных потоков, не слишком переусложнена. Выбором этого термина подчеркивается чисто техническая сторона оценки - важна отнюдь не красота или изящество программы, которые, как правило, являются следствием оригинальной и интеллектуально сильной идеи, реализованной в программе, а именно качество собственно реализации, ее профессионализм, продуманность, что и соответствует русскому слову "добротность".
При такой оценке "за бортом" остаются многие аспекты качества ПО, прежде всего касающиеся функционального соответствия программного продукта запросам клиента. Однако вместе с тем, как уже и отмечалось, хорошая оценка этой внутренней характеристики программ, составляющих программный продукт, дает определенную уверенность, что другие важные характеристики качества программного обеспечения тоже будут выглядеть неплохо.
Достоинством такого технического подхода к оценке качества программ является возможность предложить достаточно точные методы или дисциплины оценки добротности программ при инспекции и контроле качества ПО на этапе кодирования, иначе говоря - на этапе создания собственно программного текста. Недостаток этого подхода в том, что чаще всего можно говорить о добротности компонентов, но не о добротности всей программной системы в целом. Само понятие добротности нуждается в уточнении, что и будет сделано при описании критериев добротности.
Критерии добротности программ
Определив добротность программ как разумную, рациональную, непереусложненную организацию информационных потоков управления в программе и разумное построение вычислений, мы не избавились от множественности критериев оценки этой добротности. Содержание понятия добротности допускает разные классы оценок. Пытаясь оценить различные критерии добротности программ, можно свести их к следующим классам.
Количественные критерии
Количественные критерии связаны с той или иной метрикой сложности программ. В соответствии с мерой сложности по программному тексту может быть вычислена некоторая количественная характеристика или их набор, что и рекомендуется в технологиях программирования при контроле и инспекции качества. Поскольку заранее трудно говорить о том, какая сложность программы адекватна реализуемой задаче, полученную оценку можно сравнить с аналогичными продуктами, и из такого сравнения сделать вывод, переусложнена реализованная программа или нет. Следовательно, количественные критерии добротности программ, как правило, в отличие от всех последующих классов критериев, относительны - они не отвечают на вопрос о том, добротна ли данная программа, а позволяют сравнивать близкие программы и на основании сравнения определять, какая программа добротнее.
Примерами таких оценок, составляющих основу количественных критериев, являются: мера "совершенства" Холстеда [7]; оценка сложности управляющего графа программы, выражаемая цикломатическим числом; различные оценки сложности программных систем и компонентов в них и т.п. Наиболее полный обзор существующих сегодня мер сложности содержится в статье [8]. Причем некоторые меры сложности носят и абсолютный характер. Так, считается, что цикломатическое число не должно быть больше 10 (некоторые исследователи полагают, что для программ на языке Си++ предельная оценка должна быть еще ниже - 7, в противном случае управляющий граф считается излишне усложненным).
Достоинство количественных критериев в том, что с их помощью можно оценивать добротность как компонентов, так и самих систем. При модификации программы или системы можно оценивать, не изменилась ли заметно их сложность, не нарушена ли добротность.
Итак, с точки зрения количественных критериев добротная программа - это не переусложненная программа, а программа приемлемой степени сложности.
Генетические критерии
Известен следующий практический подход к оценке качества программ: программа признается хорошей, если она произведена по технологии, вызывающей доверие. Класс критериев, основанный на таком подходе - оценке добротности программ, так сказать, "по происхождению", мы назвали (может быть, не очень удачно) генетическим.
Действительно, всякая "хорошая" технология программирования предполагает хорошо продуманную дисциплину разработки, надежно переходящую от спецификации продукта к его реализации. Поскольку при такой дисциплине гарантируется - в достаточной степени - соответствие реализованной программы ее спецификации, то, привлекая широкое понятие качества ПО, качество продукта должно быть довольно высоким - лишь бы спецификация была полной и адекватной нуждам пользователя.
Для добротности интересно то, что продуманная дисциплина перехода от спецификации к программному тексту должна давать хорошую его организованность, разумную реализацию в нем потоков управления и информационных потоков.
Итак, с точки зрения генетических критериев можно быть уверенным в добротности программы или системы, если они произведены по технологии, признаваемой хорошей.
Структурные критерии
Разумная организация потока управления предполагает его ясное синтаксическое отображение в программном тексте. Подход к такому отображению сформулирован давно и выражается понятием структурированной программы. В такой программе управление представлено в виде иерархии регулярных управляющих структур, каждая из которых имеет один вход и один выход. Помимо такого простого требования, исключающего хаотичное переплетение потоков управления ("спагетти"), для добротной программы с регулярностью управления важно иметь хорошо продуманную процедурную основу (или, для объектно-ориентированного случая - систему классов). Все подобные требования к добротности программ мы относим к структурным критериям.
Ясная и четко выраженная структура управления, требуемая структурными критериями, легко сопоставляется с внешними аспектами качества программного обеспечения. Недаром большая часть известной заметки [9], положившей основу структурному программированию, посвящена тому, что в структурированных программах текст легко сопоставить с множеством отображенных в нем вычислительных процессов, иначе говоря, структурированные программы резко повышают понимаемость, а значит, и ряд других аспектов качества.
Если оценка процедурной основы или системы классов требует нетривиальных умозаключений (частично поддерживаемых некоторыми вычисляемыми мерами сложности), то структурированность программы легко усматривается из программного текста, и ее мы считаем неотъемлемым свойством добротных программ.
Итак, структурные критерии диктуют нам, что добротной признается структурированная программа с разумной организацией процедурной основы и/или системы классов.
Прагматические критерии
В работе [5] вводится и определяется специальный класс критериев добротности программ, названный прагматическими критериями. Давно было замечено, что можно формально обнаружить в программе некоторые несообразности или излишества - в [7] они названы "несовершенствами", в работе [10] - "неправдоподобностями". В статье [11] предложены правила, определяющие так называемую каноническую форму, автоматически исключающую ряд подобных несообразностей. Прагматические критерии добротности связаны с тем, что формально можно выявить некоторые свойства программы, которые содержательно трактуются как цели, достижению которых и служит программа. Такой целью может быть конечное состояние переменных, порождаемое программой, множество ее истинных (подтверждаемых программным текстом) результатов, подтверждаемые таким текстом потоки управления и информационные потоки и т.п. Развитые методы анализа программ могут обнаруживать подобные цели и находить те фрагменты и объекты данной программы, которые заведомо никак не служат достижению такой формально выявляемой цели. Наличие данных излишеств и служит основанием для того, чтобы признать программу недобротной в соответствии с прагматическими критериями. Источником таких излишеств может быть невнимание к реальным связям в программе, рудименты при неаккуратной модификации программы и т.п. - в общем, недосмотр и непрофессионализм.
Можно сказать, что добротная программа следует правилу: делать "the right things in the right way", а правильный путь подразумевает отсутствие излишеств. Итак, прагматические критерии добротности требуют, чтобы программа соответствовала своей формально выявляемой цели. Заметим, что прагматические критерии относятся скорее к компонентам, чем к системам.
В работе [5] развивается и пополняется тот список излишеств, которых не должно быть в добротных программах, а для каждого такого излишества приводится его точное определение; для ряда излишеств используются формализмы, предложенные в [11]. Для таких точных определений употребляются понятия пред- и постусловий и информационных влияний, при этом точно определяются условия нарушения добротности - наличие какого-либо излишества. Заметим, что все определения даются для структурированных программ, а только их мы и считаем добротными.
Очевидно, что само понятие формально выявляемой цели может быть различным, но и излишества тоже весьма разнообразны. Поэтому в работе [5] прагматические критерии группируются по нескольким видам требований к добротным программам.
- Целевая направленность. В этом случае под целью понимается множество допустимых конечных состояний памяти переменных. Вычислительный процесс за счет применения операторов программы получает последовательность состояний - от начального до конечного, а программа, описывающая множество таких процессов, не может содержать операторы, всегда сохраняющие исходное (для оператора) состояние, в противном случае мы не движемся к цели, а топчемся на месте. Достаточно простой пример нарушения этого вида требований - наличие оператора x := y, если известно, что всегда перед оператором равенство x = y выполняется.
- Структурная целесообразность. Цель - поддержка видимой структуры управления, а нецелесообразностью считается наличие циклов, заведомо не выполняемых более одного раза, или таких, эффект которых не требует повторения, а также операторов ветвления с заведомо не выполняемыми ветвями. Иначе говоря, структурный оператор управления, если уж он употреблен, должен действительно задавать все возможные по общей семантике оператора потоки управления.
-
Оправданная выстроенность вычислений. Целью здесь является некоторое разумное размещение вычислительного оператора в вычислительном процессе - там, где его присутствие необходимо, а не там, где он, хотя и корректно влияя, выполняется чаще, чем надо. Иначе говоря, выбор размещения оператора в некотором участке повторения должен быть оправдан. Нарушение этого вида требований возникает, например, когда оператор помещен в цикл, хотя без ущерба для корректности может быть оттуда вынесен.
- Вычислительная неизбыточность. Цель - выработка значений тех переменных, которые формально могут быть определены как результаты программы, а излишеством считается присутствие вычислений и объектов, никак не влияющих на эти результаты.
- Разумная организация информационных потоков. Здесь целью является поддержание обнаруженных информационных потоков, а отклонением от цели - "дурная" (хотя и правильная) организация таких потоков. В следующей части статьи будет дана точная формулировка этого вида требований.
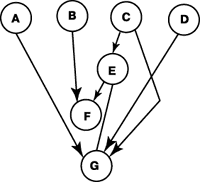
Рис. 1. Информационный граф
Добротность информационных потоков: точная постановка
Очевидно, что хорошая организованность, ясность и наглядность информационных потоков - это свойство программ, которое существенно влияет на ряд внешних характеристик качества ПО: программа должна быть простой для понимания, а ее тестируемость, переносимость, модифицируемость повышается. Содержательно в представление о хорошей организованности информационных потоков мы будем вкладывать следующий смысл.
Во-первых, информационные потоки не должны быть неоправданно перепутаны. Точно так же, как для структурированных программ мы не допускаем "спагетти" из потоков управления, для добротных программ мы требуем отсутствия "спагетти" информационных потоков - последовательность операторов должна быть выстроена таким образом, чтобы не связанные между собой информационные потоки проходили через различные подпоследовательности входящие в исходную. Поясним простым примером, нарушающим такое требование:
x:(f1(y); a:(f2(b); z:(f3(x); c:(f4(a); u:(f5(z, c)
Здесь для вычисления u требуется получить значения z и c, однако вычисления организованы таким образом, что сначала находится нужное для z значение x, потом вычисление переключается на поиск значения a (нужное для c), затем вспоминаем про z и только потом возвращаемся к вычислению c. Ясно, что более разумной последовательностью будет, например:
x:(f1(y); z:(f3(x); a:(f2(b); c:(f4(a); u:(f5(z,c).
Во-вторых, для понимания и осмысления информационных потоков важно убедиться в их подтвержденности - в том, что переменная всегда инициализируется до ее использования. Если инициализация происходит внутри некоторого оператора, допускающего альтернативные маршруты управления - в операторе ветвления или цикла, - то для видимой подтвержденности информационных потоков следует считать, что оператор в целом гарантирует эту подтвержденность и на всех возможных альтернативах такая инициализация происходит. Подобное требование по отношению к операторам ветвления было сформулировано в работе [11] и заключалось в том, что если переменная инициализируется хотя бы на одной из ветвей этого оператора, то она должна инициализироваться и на остальных ветвях. Согласитесь, что, хотя такое требование и исключает программистские трюки и ограничивает свободу, столь желанную для некоторых программистов, это разумная дисциплинарная мера, способствующая ясности информационных потоков. С этой точки зрения фрагмент:
if Q1 then a:= f1(x) else b:=f2(x); if not Q1 then a:=f3(x) else b:=f4(x),
где a и b инициализируются, хотя и обеспечивает подтвержденность потока, выглядит нехорошо. Итак, будем требовать равномерной - на всех маршрутах - инициализации переменных, если эти переменные - не внутренние для одного или нескольких маршрутов управления.
Таким образом, информационные потоки считаются добротными, если они регулярны (независимые потоки не переплетаются) и если существует видимая подтвержденность потоков (переменная инициализируется на всех альтернативах потока управления).
Для точного определения критериев добротности информационных потоков будем использовать простую, но вполне подходящую для данного случая модель линейных схем, введенную в работе [12]. В этой модели программа представляется линейной последовательностью операторов S1 S2 ? Sn , причем для каждого Si должны быть известны аргументное множество A(Si), результатное множество R(Si) и сильно результатное множество R((Si) (подмножество R(Si), включающее те результаты, которые обязательно будут выработаны при выполнении Si). Все эти множества являются подмножествами множества переменных программы, а их смысл ясен из названия. В модели определены естественные правила образования аргументного, результатного и сильно результатного множества подпоследовательности Si ? Sj (j>i) по соответствующим множествам входящих в нее операторов. Для обозначения подпоследовательности операторов, предшествующих некоторому Si , используется обозначение -Si, а для подпоследовательности операторов, следующих за ним, - -Si. Несмотря на простоту, модель сохраняет свою полезность. Оператор Si может соответствовать и простому оператору (присваивания или вызова) и управляющей композиции операторов (циклу или ветвлению).
В точной формулировке требования на регулярность информационных потоков будем рассматривать только относительно линейных последовательностей операторов. В структурированных программах ветви оператора ветвления или тела циклов - именно такие последовательности. Пытаться же рассматривать информационные потоки, которые проходят через операторы как вне, так и внутри структурных операторов управления (ветвлений и циклов), было бы неразумно - следование операторам в этих случаях подчиняется не только необходимости поддержки нужных информационных влияний, но и логике управления.
Итак, мы рассматриваем некоторую линейную схему:
T=S1 ... Sn.
Будем говорить, что Sj зависит от Si (i
а) существует такая переменная x, что x ? R(Si), xP A(Sj) и x ? R9(Si+1 ... Sj-1), иначе говоря, значение x, выработанное Si, доходит до Sj , где и используется;
б) существует такая переменная x, что x ? R(Si), x P R(Sj)R9(Sj) и x ? R(Si+1 ... Sj-1), иначе говоря, значение x, выработанное Si, доходит до Sj, а Sj меняет или не меняет это значение; если не меняет, то значение x, выработанное Si, проходит дальше, а значит, его можно считать псевдоаргументом Sj при выработке x.
Информационным графом I для последовательности T является ориентированный граф, вершины которого - операторы T (вершины помечены оператором из T ), а из i-й вершины существует дуга в j-ю, если Sj зависит от Si.. Информационным потоком I(Si ) оператора Si назовем подграф графа I, включающий все вершины I, из которых существует путь в i-ю, в том числе и саму эту вершину. Реализацией I(Si) назовем подпоследовательность T(Si)=S1,...,Si, где 1 - минимальный номер вершины в I(Si). Два информационных потока I(Sn) и I(Sm) будем называть независимыми, если они не содержат общих вершин и пересекающимися, если они содержат общие вершины и ни один из них не является подграфом другого. Информационный поток I(Si), содержащий только i-ю вершину, назовем тривиальным. Усеченной реализацией I(Sn) по отношению к пересекающимся с ним I(Sm) назовем такую подпоследовательность T(Sn:Sm), для которой минимальный номер в подпоследовательности берется без учета общих для них вершин (операторы, им соответствующие, могут входить в T(Sn:Sm), но эта подпоследовательность не может начинаться с них).
Заметим, что сопоставить линейную схему со структурированной программой или ее линейным фрагментом, таким, как ветвь оператора ветвления или тело цикла, нетрудно, если считать каждый из находящихся в последовательности структурных операторов управления единым оператором. Для этого нужно только достоверно определить множества A(S), R(S) и R((S) , что методы анализа программ позволяют сделать. Поэтому не имеет смысла различать программу или ее линейные фрагменты и соответствующие им линейные схемы.
На основании сказанного можно заключить, что информационные потоки в программе с точки зрения регулярности добротны, если как для нее, так и для всех ее линейных фрагментов любого уровня вложенности справедливо следующее:
а) реализация любого информационного потока I(S) не содержит операторов, относящихся к независимому по отношению к I(S) информационному потоку;
б) усеченная реализация I(Sn) по отношению к пересекающимся с ним I(Sm) не содержит операторов, для которых соответствующие вершины принадлежат I(Sm) и не принадлежат I(Sn).
Очевидно, что нарушение условия (а) приводит к неоправданному переплетению информационных потоков. Условие (б) нуждается в некотором пояснении. Рассмотрим информационный граф (рис.1) и, чтобы рассмотреть различные последовательности операторов, вершины I пометим именами операторов. Очевидно, что граф состоит из двух пересекающихся информационных потоков I(F) и I(G) и вложенного в них нетривиального информационного потока I(E). Рассматривая различные корректные последовательности операторов, можно заметить, что:
- информационные потоки в последовательности ABCDEFG не являются добротными, так как, начав с вычисления A, нужного для G, мы бросаем вычисления для G и ведем вычисления для E (по условию (б) усеченная реализация T(G:F)= ABCDEFG содержит B и F , не принадлежащие I(G));
- информационные потоки в последовательности ABCDEGF тоже не являются добротными хотя бы потому, что в усеченную реализацию T(G:F) вклинилось B, что содержательно излишне для G и ведет к ненужному переплетению;
- информационные потоки в последовательности BCEFADG добротны, ибо мы действительно вычисляем все нужное для F, а потом довычисляем нужное только для G (и, действительно, усеченные реализации T(F:G)= BCEF и T(G:F)= ADG не содержат ничего постороннего);
- информационные потоки в последовательности CEDAGBF также добротны, так как усеченные реализации T(G:F)=DAG и T(F:G)= BF не содержат ничего постороннего;
- информационные потоки в последовательности CDEAGBF не добротны, так как T(E)=CDE содержит D - оператор независимого от I(E) тривиального информационного потока I(D) - нарушение условия (а) (с точки зрения условия (б) здесь все в порядке).
Содержательно отсутствие переплетений означает, что операторы в программе сгруппированы разумно, в соответствии с реальными информационными связями, а значит, при рассмотрении программы не будет возникать лишних вопросов: "А это зачем? Для чего?". Заметим, кстати, что последовательные программы с добротными с точки зрения регулярности информационными потоками без дополнительной перестановки операторов естественно разбиваются на процессы, выполняемые параллельно работающими процессорами.
Требования к видимой подтвержденности потока формулируются следующим образом.
Во-первых, инициализация переменной должна происходить на прямом пути от начала программы к операторам, использующим эту переменную как аргумент. Здесь мы запретим такие хитрые трюки, как инициализация переменной в операторах, формально следующих за использующими эту переменную операторами, если сначала путь к использующим операторам не проходится, а срабатывает только на некотором повторении. Пример такого трюка - фрагмент
while p do begin if q then x:=f(a); a:=f2(x,b) end,
где a не инициализировано до цикла (x инициализировано), но при первом исполнении тела цикла значение q есть ложь. Не сразу становится ясно, что q именно таково, а без этого программа кажется бессмысленной.
Во-вторых, будем требовать, чтобы инициализация происходила на всех ветвях оператора ветвления, а в теле цикла - только тогда, когда цикл заведомо выполняется хотя бы один раз. Исключением может быть случай, когда инициализируемое значение локально используется только в данной ветви или теле цикла соответственно.
Для каждого оператора S программы можно построить линейную схему(S, которая соответствует операторам, предшествующим S в простом (без повторений) пути от начала программы, и линейную схему S, которая соответствует операторам, следующим за S в простом пути до завершения программы. Структурные операторы (циклы и ветвления) раскрываются в S и S только тогда, когда S содержится в них, иначе каждый из них представляется в этих линейных схемах одним оператором.
С учетом этого точная формулировка видимой подтвержденности потока такова.
- n Если существует переменная x , такая, что x ? A(-S), то x ? R (-S).
- n Если оператор S есть оператор ветвления с ветвями SL1,..., SLn (SLi - соответствующая линейная схема i-й ветви), и переменная x такова, что x ? A(-S), то должно быть справедливо хотя бы одно из следующих условий:
а) x ? ш R(SLi), иначе говоря, x не инициализируется ни на одной ветви;
б) x P щ R(SLi) , иначе говоря, x инициализируется на всех ветвях;
в) x P R (SLi) и x ?A(-S), иначе говоря, инициализируемое значение x используется только внутри ветви SLi (согласно правилам образования аргументных множеств это не исключает использования x в последующих операторах, но таким операторам должно предшествовать обязательная выработка значений x).
- Если оператор S есть оператор цикла с телом SL (соответствующая линейная схема) и x ? R(-S), то должно быть справедливо хотя бы одно из условий:
а) x ? A(SL) - x не инициализируется в цикле;
б) x ? R(SL) и гарантируется, что при первом исполнении S он исполняется как минимум один раз (инициализируется всегда);
в) x ? R(SL1) и x ? A (-S) - локальное использование инициализированного значения (см. также пояснения к 2в).
Если эти условия для программы выполняются, то ее информационные потоки считаются добротными с точки зрения видимой подтвержденности потока. Конечно, эти требования несколько ограничивают свободу программиста, но, на наш взгляд, они соответствуют хорошей дисциплине и культуре программирования.
Итак, введенное в статье понятие добротности программ - подчеркнем еще раз - является, на наш взгляд, важной внутренней характеристикой, которая хорошо коррелирует с внешними характеристиками качества программного обеспечения.
Введенная классификация критериев добротности не ортогональна, различные классы критериев не являются независимыми. Многими отмечалось, что признаваемые хорошими технологии программирования (а это основа генетических критериев), как правило, приводят к созданию структурированных программ (что требуется структурными критериями). Еще в работе [7] отмечалось, что "несовершенства" (иначе говоря, нарушения прагматических критериев) ухудшают оценки сложности (что относится к количественным критериям). В формулировке прагматических критериев отмечалось, что добротные программы должны быть структурированными (следование структурным критериям). Вместе с тем все классы критериев дополняют друг друга при оценке программ на добротность.
Неявно все эти классы критериев добротности используются при инспекции и контроле качества программного обеспечения. Если генетические и структурные критерии практически не нуждаются в специальных инструментах, то инструменты, соответствующие проверке количественных критериев, существуют и используются. В каком-то смысле сверхзадача этой статьи - убедить в необходимости и полезности инструментов поддержки проверки прагматических критериев. Некоторые анализаторы программ (например OSA [13] ) уже содержат проверки ряда прагматических критериев. Во всяком случае, современное состояние методов анализа и понимания программ позволяет создать инструменты, поддерживающие все перечисленные здесь виды требований к добротности программ в соответствии с прагматическими критериями.
Литература
- P. Crosby. Quality is Free/McGraw-Hill, N.Y., 1979.
- P. Nesi. Objective Quality, 1995//Objective Software Quality, LNCS № 926, Springer, 1995, p. 1-9.
- I. Sommerville. Software Engineering/Addison-Wesley Pub. Co., 1996.
- В. Липаев. Качество программного обеспечения//Финансы и статистика, М., 1983.
- И. Поттосин. "Хорошая программа": попытка точного определения понятия//Программирование.-1997. - № 2. - С.3-17.
- I.V. Pottosin. A "Good Program": An Attempt at an Exact Definition of the Term.//Programming and Computer Software. - v. 23, № 2. - 1997. - p.59-69.
- M. Halstead. Elements of Software Science/Elsevier, N.Y., 1977. (Русск. перевод: Холстед М.Х. Начало науки о программах. Финансы и Статистика, М., 1981).
- С. Черноножкин. Меры сложности программ (Обзор)//Системная информатика, № 5, Новосибирск: Наука, 1996, Вып. 5. - с.188-227.
- E.Dijkstra. Go to Statement Considerеd Harmful//Commun. ACM. - 1968. - V. 11, № 3, - p.147-148.
- V. Kasjanov, I. Pottosin. Application of optimization techniques to correctness problems//Consructing Quality Software. - North-Holland, 1978. - pp.237-248.
- S.Pan, R.G.Dromey. Bejond Structured Programming//Proc. ICSE-18. -Berlin. -pp.268-278.
- И.В. Поттосин. К обоснованию алгоритмов оптимизации программ //Программирование. - 1973. - № 2. -С.3-13.
- С. Куксенко, В. Шелехов. Статический анализатор семантических ошибок периода исполнения//Программирование. - 1998 (в печати)
