Одно из быстро развивающихся направлений в геометрическом моделировании и машинной графике - называемое "функциональное представление". Это одна из немногих в МГ областей, где приоритетными признаны работы российских специалистов. В статье дается краткий обзор выполненных за последние годы работ, результаты которых опубликованы в ряде международных журналов и трудах международных конференций. Этот обзор вошел в курс "Неявно заданные поверхности в геометрическом моделировании и компьютерной графике", который был представлен в этом году на конференции SIGGRAPH"96. Полный иллюстративный материал к данной статье можно найти на странице сервера [1], который был признан на конкурсе "Eurographics"96 WWW competition" лучшим по разделу инновационных технологий.
Функциональное представление (F-rep) определяет геометрический объект как единое целое с помощью одной вещественной непрерывной описывающей функции нескольких переменных в виде F(X) > 0 [2]. Традиционное использование неявных функций в компьютерной графике охватывает: скелетоны (skeletons), генерирующие скалярные поля или так называемые "капельные объекты" (blobby objects); примитивы конструктивной геометрии твердых тел (CSG); алгебраические отсеки поверхностей в граничном представлении.
F-rep является попыткой продвижения к более общей схеме моделирования с использованием вещественных функций. F-rep объединяет многие разные по природе модели, в частности, классические неявно заданные примитивы, объекты на базе скелетонов, теоретико-множественные твердые тела, заметания, воксельные объекты, параметрические и процедурные модели [2].
Система понятий, используемая при моделировании, включает множества объектов, операций и отношений. Каждая операция должна быть замкнута на представлении, генерируя в качестве результата непрерывную вещественную функцию. В статье мы приведем краткое описание преобразований описывающей функции для базовых операций: теоретико-множественных, гладкого сопряжения, офсеттинга, биективного отображения, проецирования, декартова произведения и метаморфозиса. Будут введены также отношения включения, принадлежности точки и пересечения. Далее будет дана характеристика более сложных операций для F-rep: заметание движущимся твердым телом, деформации при помощи алгебраических сумм, моделирование трехмерной текстуры и столкновений тел. Гибкость и универсальность данного подхода иллюстрируется примерами приложений.
Геометрические объекты
Мы рассматриваем геометрические объекты как замкнутые подмножества Эвклидова пространства En, определяемые описывающей функцией F(X) > 0, где F - непрерывная вещественная функция, и X = (x1, x2,..., xn) - задаваемая координатными переменными точка в En. Здесь F(X) > 0 задает точки внутри объекта, F(X) = 0 - точки на границе и F(X) < 0 - точки, лежащие снаружи и не принадлежащие объекту. Мы не налагаем особо строгих условий на функции, ограничиваясь требованием наличия по крайней мере C0 непрерывности. Функции могут быть определены формулами или с помощью вычислительных процедур. Таким образом определенные геометрические объекты, вообще говоря не представляют регуляризованные конструктивные твердые тела. Они могут иметь границу с участками, не смежными с внутренностью объекта. Общее определение объекта дается в многомерном пространстве, что позволяет выбирать пространство нужной размерности в каждом конкретном случае.
При проектировании конкретной системы моделирования может быть определено некоторое конечное множество объектов-примитивов. Однако концептуально это не обязательно, что позволяет иметь пустое множество объектов в предположении, что пользователь определит их сам либо в символьном виде с помощью формул, либо посредством вычислительных процедур. Такой подход позволяет унифицировать очень разные виды моделей твердых тел при условии, что удается найти функциональные представления для них или конвертировать уже существующие объекты в желаемую форму. Таким образом, например, мы можем совместно использовать в одной модели примитивы конструктивной геометрии, неявно заданные объекты свободной формы, заметенные твердые тела и воксельные объекты.
Базовые операции
Теоретико-множественные операции определяются в аналитическом виде с помощью разработанной В.Л.Рвачевым теории R-функций [3]. При этом результирующий объект включает граничные точки, что соответствует операциям трехзначной логики над предикатом принадлежности точки. Существует несколько систем R-функций, каждая из которых имеет свойство замкнутости. Наиболее часто используется следующая система (f1 и f2 - функции, определяющие исходные геометрические объекты):
· для объединения:
f1 | f2 = (1/(1+a) * (f1 + f2 + sqrt(f12 + f22 - 2*a*f1*f2));
· для пересечения :
f1 & f2 = (1/(1+a) * (f1 + f2 - sqrt(f12 + f22 - 2*a*f1*f2));
· для отрицания
~f = -f;
· для вычитания:
f1 f2 = f1 & (-f2).
Здесь a = a(f1,f2) - произвольная непрерывная функция такая, что:
-1 < a(f1,f2) <= 1,
a(f1,f2) = a(f2,f1) = a(-f1,f2) = a(f1,-f2).
На практике используют два важных частных случая:
1. a = 1; в этом случае
f1 | f2 = max(f1,f2);
f1 & f2 = min(f1,f2)
Основное ограничение этих широкоизвестных минимаксных операций заключается в разрывности С1 в точках, где f1 = f2, что может вызвать нежелаемые результаты при последующих операциях над объектом.
2. a = 0; в этом случае
f1 | f2 = f1 + f2 + sqrt(f12 + f22);
f1 & f2 = f1 + f2 - sqrt(f12 + f22).
Эти функции имеют разрывы C1 только в точках, где f1 = f2 = 0 и в то же время достаточно просты, что и обусловливает их наиболее широкое использование. Существуют и системы R-функций, обеспечивающие Ck непрерывность.
Теоретико-множественные операции гладкого сопряжения (blending) генерируют сглаженные ребра конструктивных твердых тел с добавленным или удаленным материалом. Мы предложили для них следующее выражение:
B(f1,f2) = R(f1,f2) + d(f1,f2),
где R(f1,f2) - это соответсвующая R-функция, и d(f1,f2) - сходная с Гауссианом функция смещения. В частности, возможно следующее выражение
d = a0 / (1 + (f1/a1)2 + (f2/a2)2),
где a0, a1, a2 - параметры, управляющие результирующей формой. На рис.1 изображен объект, смоделированный с помощью теоретико-множественных операций и операций гладкого сопряжения.

Рисунок 1.
Кресло, смоделированное с помощью теоретико-множественных операций
и операций гладкого сопряжения.
Офсеттинг (offsetting) сжимает или расширяет исходный объект. В работе [2] мы обсуждаем три различных формы офсеттинга:
1) офсеттинг постоянного значения
Foffset1(f) = f(X) + Const;
2) офсеттинг вдоль нормали
Foffset2(f) = f(X+D*N),
D - заданное расстояние, N - вектор-градиент функции f.
3) офсеттинг постоянного радиуса
Foffset3_1(f) = max(f(X")) или
Foffset3_2(f) = min(f(X")),
X" - вектор координат точки, принадлежащей сфере заданного радиуса с центром в X.
Офсеттинг вдоль нормали иллюстрируется рис.2, где величина смещения вдоль нормали контролируется набором данных о глубине.

Рисунок 2.
Офсеттинг вдоль нормали, где величина смещения контролируется набором
данных о голове, задающих глубину.
Декартово произведение - это операция, увеличивающая размерность. В частности, с ее помощью можно генерировать 3D твердое тело как декартово произведение 2D твердого тела и отрезка линии. В терминах R-функций это выражается в виде:
f3(x, y, z) = f1(x, y) & f2(z)
где f1(x, y) описывает планарное твердое тело и f2(z) = (z - z1) & (z2 - z) описывает отрезок [z1, z2] вдоль оси z.
Биективное отображение служит для определения деформаций исходных объектов. Если Фi определяется преобразованиями координат:
xj" = gi(x1, x2, ..., xn), j = 1, ..., n
где gi - непрерывная функция, имеющая обратную функцию qi, то
Fbiject(f) = f(q1(x1", x2",... ,xn"), ..., qn(x1",..., xn")) > 0.
Примеры таких преобразований: изгиб (bending), кручение (twisting), сжатие-расширение (tapering), а также отображение из цилиндрической в декартову систему координат.
Важный частный случай - аффинные преобразования
X" = A X + C:
Faff(f) = f(B (X"-C)),
где B - обратная матрица A.
Метаморфозис (metamorphosis) - это бинарная операция над объектами, определенными в пространстве En-1. Результирующий объект определен в En и описывается как взвешенная интерполяция между двумя определяющими функциями f1 и f2:
f3(x1, x2,..., xn) = f1(x1, x2, ..., xn-1) * (1 - g(xn)) + f2(x1, ..., xn-1) * g(xn)
где g(xn) - положительная непрерывная функция, g(xn0) = 0, g(xn1) = 1.
В результате при различных значениях xn получается множество промежуточных форм между двумя заданными объектами.
Отношения
Отношения включения и принадлежности (внутри/на границе/вне) для точки и геометрического объекта могут быть выражены непосредственно в терминах определяющей функции. Отношение пересечения (столкновения) может быть вычислено как свойство непустоты множества пересечения двух объектов.
Сложные операции
Заметание движущимся объектом
Заметание (sweeping) движущимся твердым телом является одной из давних и трудных проблем в твердотельном моделировании. Мы свели проблему описания заметенного тела к одномерному поиску глобального экстремума по параметру, задающему движение [3]. Это позволяет использовать произвольные изменяющиеся во времени формы и конструктивные твердые тела в качестве генераторов с произвольно параметризованным движением и самопересечениями (рис.3).

Рисунок 3.
Заметание движущимся и вращающимся твердым телом (объединением шара
и эллипсоида).
Деформации с помощью отображений пространства на основе особенностей
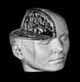
В работе [4] представлен метод для определения деформаций на основе произвольных контрольных точек, связанных с особенностями (features) объекта. Для интерполяции смещения контрольных точек используется объемный сплайн. На рис.6 представлен пример применения этого метода для моделирования выражений человеческого лица, где были сдвинуты пять контрольных точек, а восемь точек были фиксированы, чтобы локализовать деформации (срез на рис.4а демонстрирует воксельную природу данных, на основе которых была сгенерирована исходная голова).
 (a)
(a)
 (б)
(б)
Рисунок 4.
(а): Исходная (воксельная) голова и (б): выражение лица, смоделированное
с помощью отображений пространства на основе особенностей.
Деформации с помощью алгебраических сумм
Для управления деформациями, определяемых положением произвольных точек, мы предложили в [4] использовать алгебраические суммы:
f3(x, y ,z) = f1(x, y, z) + disp(x, y, z),
где disp - функция смещения такая, что в каждой i-ой контрольной точке
disp(xi, yi, zi) = - f1(xi, yi, zi),
что гарантируется использованием одного из методов интерполяции. Получаемая в результате новая поверхность проходит через все заданные контрольные точки. С помощью такого подхода могут моделироваться небольшие локальные деформации, эффекты уколов и царапин. Он также может быть использован для реконструкции твердого тела из точек, произвольно расположенных на поверхности (рис. 5).
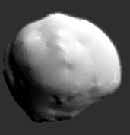
Рисунок 5.
Реконструкция Фобоса (спутника Марса) из точек, произвольно расположенных
на поверхности с помощью алгебраических сумм с использованием объемного
сплайна.
Визуализация
Еще в 1986 г. был предложен и реализован алгоритм полигонизации изоповерхности [5]. Он свободен от топологических неопределенностей, которые столь существенны для алгоритма марширующих кубов (marching cubes). Для обнаружения гиперболических дуг на гранях кубических ячеек используется трилинейная интерполяция, после чего конструируется граф связности ребер. Параллельная версия алгоритма реализована на сети рабочих станций с системой PVM и на транспьютерной сети. Мы также используем традиционный алгоритм трассировки лучей для генерации полутоновых изображений.
Одно из достоинств Функционального представления - это возможность гибкого задания режима визуализации с помощью концепции "геометрических типов", определяющих семантику координатных переменных. В частности, координатным переменным xi могутназначаться следующие геометрические типы:
Заметим, что геометрические типы "constant" и "g" могут также назначаться и самой определяющей геометрический объект функции. В нормальном режиме нулевая константа определяет границы объекта.
Взаимодействие с пользователем
Взаимодействие пользователя с моделирующей системой строится на принципах эмпирического (или исследовательского) моделирования, которое акцентирует значимость интерактивных экспериментов пользователя с моделью. Высоко-уровневый геометрический язык точечных множеств HyperJazz позволяет реализовать пошаговую итеративную разработку функциональной модели в интерактивном режиме, не накладывая никаких ограничений на ее оперативную модификацию. Опираясь на парадигму определительного программирования (definitive programming), язык поддерживает в стиле, сходном с объектно-ориентированным, все основные понятия F-rep, позволяя описывать геометрические объекты, преобразования и отношения, и реализуя механизм синтеза сложных объектов. Язык обеспечивает полную расширяемость системы путем интерактивного ввода символьных описаний новых объектов-примитивов и операций, что в принципе позволяет каждому пользователю создать и использовать свою персональную систему геометрического моделирования. Язык показал высокую эффективность при обучении студентов геометрическому моделированию. Более подробное описание можно найти в [6,7].
Приложения
Эстетический дизайн
Параметризованные операции, в частности, теоретико-множественное гладкое сопряжение, обеспечивают эффективный контроль над получаемыми формами. Однако, непосредственное применение таких операций в эстетическом дизайне может оказаться неорганичным: дизайнер предпочитает определять сразу всю форму результирующего объекта посредством линии, вводимой от руки, вместо задания числовых значений параметров. Точки, находящиеся на этой линии, используются для вычисления параметров операций с помощью решения системы нелинейных уравнений. На рис.6 иллюстрируется использование этого метода для теоретико-множественного гладкого сопряжения.
 (a)
(a)
 (б)
(б)
Рисунок 6.
(а): Корпус и днище фужера, которые должны быть сопряжены с помощью
вводимой рукой дизайнера линии; (б) Результат операции гладкого сопряжения
на основе вычислительных параметров.
Моделирование трехмерной текстуры
Моделирование трехмерной текстуры основано на расширенном использовании примитива "твердый шум" (solid noise), определяемого с помощью псевдо-случайных функций трех переменных. Если функция твердого шума непрерывна, то она определяет некий 3D примитив, который может быть использован как аргумент в любой из операций, замкнутой на F-rep. Таким образом могут быть смоделированы (в виде функций!) различные виды трехмерных текстур, в частности, мох, снег, шерсть, волосы [8]. Различные прически могут быть смоделированы при помощи процедурно определенных вещественных функций с использованием твердого шума, заметания, офсеттинга и нелинейного отображения пространства (рис.7).
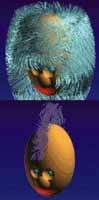
Рисунок 7.
Выращивание волос и создание прически с помощью нелинейного отображения
пространств и теоретико-множественных операций.
Моделирование операций для станков с ЧПУ
Применение теоретико-множественных операций к движущимся твердым телам может быть использовано в моделировании операций в станках с числовым программным управлением (NC machining). Результат определяется как теоретико-множественное вычитание твердого тела, заметенного движущимся инструментом, из модели заготовки. Комбинация трехмерного текстурирования и ЧПУ-операций, представленная на рис.8, показывает преимущества, которые можно извлечь из фундаментального свойства замкнутости операций на функциональном представлении.
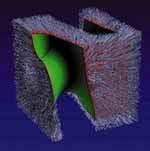
Рисунок 8.
Иллюстрация свойства замкнутости операций в F-rep
с использованием комбинации трехмерного текстурирования с последующими
операциями ЧПУ.
Реконструкция
Для реконструкции твердых тел из точек, произвольно расположенных на некоторой поверхности (рис.5), и из сечений (рис.9) используются деформации с помощью алгебраических сумм. Для случая заданных сечений, техника деформаций применяется к каждому из сечений по отдельности, и затем твердое тело в целом реконструируется с помощью операции метаморфозиса между каждой парой смежных сечений [9]. Другой тип реконструкции: "стандартный" зуб отображается на зуб с полостью с тем, чтобы восстановить его отсутствующую часть с последующей генерацией формы пломбы. Два зуба подгоняются с помощью основанного на особенностях отображения пространств, как это было показано выше.
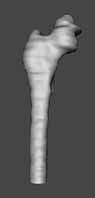
Рисунок 9.
Берцовая кость человека, реконструированная из сканированных сечений.
Моделирование столкновений
В ряде приложений: динамика столкновений тел и небесная механика, молекулярная динамика, компьютерные игры возникает проблема моделирования поведения взаимодействующих тел, имеющих нерегулярную форму. Тела могут иметь переменную ориентацию в пространстве; в результате столкновений некоторые тела могут прилипать друг к другу, меняя свою геометрическую форму. Алгоритм обнаружения столкновений, описанный в [10], основан на отношении пересечения и использует псевдослучайные последовательности Соболя и спиральный квадратичный поиск для обнаружения неотрицательных величин функции, определяющей пересечение. При этом для определения области, в которой ведется поиск, используются ограничивающие тела сферы (bounding spheres).
Заключение
При использовании Функционального представления иногда возникают проблемы. Прежде всего, вычисление определяющей функции в заданной точке часто оказывается весьма трудоемкой задачей. Особенно явно это выражено в случае использования R-функций с квадратными корнями. Отметим, что полутоновые изображения из приведенных в статье иллюстраций получены на рабочей станции Silicon Graphics Indigo 2 с помощью алгоритма трассировки лучей. При этом среднее время вычисления с двойной точностью изображения 200 х 200 составляло 20 - 90 сек. Хотя мощные графические станции и обеспечивают приемлемое время отклика, полностью вычислительные проблемы могут быть сняты при использовании компьютеров с параллельной архитектурой, особенно если некоторые процедуры будут реализованы аппаратно. Параллельная реализация алгоритма полигонизации изоповерхности увеличивает эффективность счета практически линейно по отношению к числу процессоров.
Другая проблема связана с возникающей на практике необходимостью получения Функционального представления из Граничного представления (B-rep). Прямое преобразование затруднительно, поэтому предлагается сначала конвертировать B-rep в конструктивное представление со стандартными - нерегуляризованными теоретико-множественными операциями, а затем перейти к F-rep с R-функциями. Данная проблема еще нуждается в дальнейшем исследовании.
К сожалению, не существует прямого соответствия между F-rep и параметрическими представлениями. Ввиду того, что параметрические поверхности очень удобны для интерактивного геометрического проектирования, мы пытаемся инкорпорировать их в Функциональное представление, которое требует от пользователя определения модели довольно абстрактным способом. Используя символьный интерфейс, пользователь может произвольным образом расширять систему, определяя новые объекты-примитивы и операции. Важная и пока не полностью решенная проблема - это гармоничное интегрирование как графического, так и символьного интерфейса.
Функциональное представление открыло богатые возможности для дальнейшего развития в моделировании твердых тел и в машинной графике. Главные результаты на сегодняшний день - это интеграция нескольких различных моделей в рамках единого подхода; универсальность в обработке статических, динамических и многомерных объектов; разрушение барьера между твердыми и деформируемыми телами; полная расширяемость системы моделирования. Дальнейшее развитие видится в наращивании набора операций, замкнутых на F-rep, в разработке базового ядра распределенной системы моделирования в рамках WWW, а также в поиске и решении прикладных задач, требующих сложных настраиваемых средств геометрического моделирования.
Литература
[1] Shape Modeling and Computer Graphics with Real Functions,
WWW site at URL: http://www.u-aizu.ac.jp
/public/www/labs/sw-sm/FrepWWW/F-rep.html
[2] Pasko A., Adzhiev V., Sourin A., Savchenko V. Function representation in geometric modeling: concepts, implementation and applications, The Visual Computer, vol.11, # 8, 1995, pp. 429-446.
[3] Sourin A., Pasko A. Function representation for sweeping by a moving solid, IEEE Transactions on Visualization and Computer Graphics, vol.2, # 1, March 1996, Special issue on solid modeling, pp. 11-18.
[4] Pasko A.A., Savchenko V.V. Algebraic sums for deformation of constructive solids, Third ACM Symposium on Solid Modeling and Applications, C.Hoffmann and J.Rossignac (Eds.), Salt Lake City, Utah, USA (May 17-19, 1995), ACM Press, 1995, pp. 403-408.
[5] Пасько А.А., Пилюгин В.В., Покровский В.Н. Геометрическое моделирование в задаче анализа функций трех переменных, Сообщение ОИЯИ Р10-86-310, Дубна, 1986. Publication in English: Computers and Graphics, vol.12, # # 3/4, 1988, pp. 457-465.
[6] Adzhiev V.D., Beynon W.M. and Pasko A.A. Interactive geometric modelling based on R-functions: an agent-oriented approach, Set-theoretic Solid Modeling: Techniques and Applications, CSG 94 Conference Proceedings, Information Geometers, Winchester, UK, pp. 253-272, 1994.
[7] Adzhiev V.D., Pasko A.A., Sarkisov A.V. "HyperJazz" project: development of geometric modelling systems with inherent symbolic interactivity, Set-theoretic Solid Modeling: Techniques and Applications, CSG 96 Conference Proceedings, Information Geometers, Winchester, UK, pp.183-198, 1996.
[8] Sourin A., Pasko A., Savchenko V. Using real functions with application to hair modelling, Computers and Graphics, vol.20, # 1, Pergamon, 1996, pp. 11-19.
[9] Savchenko V.V., Pasko A.A., Okunev O.G., Kunii T.L. Function representation of solids reconstructed from scattered surface points and contours, Computer Graphics Forum, vol.14, # 4, 1995, pp. 181-188.
[10] Savchenko V.V., Pasko A.A. Collision detection for functionally defined deformable objects, The First International Workshop on Implicit Surfaces (Grenoble, France, April 18-19, 1995), B.Wyvill and M.-P. Gascuel (Eds.), Eurographics-INRIA, 1995, pp. 217-221.
