Известно, что наиболее эффективен параллельный код, ориентированный на конкретную вычислительную систему, что, однако, увеличивает риск повторного переписывания программы при переходе на другую архитектуру. Мало того, зачастую ранее используемые методы плохо поддаются распараллеливанию или не обеспечивают достижения требуемых критериев, например, погрешности вычислений, и тогда приходится создавать новые алгоритмы, адаптированные к специфике предоставляемых вычислительных ресурсов.

Сегодня используются разнообразные параллельные архитектуры и нет никакой гарантии, что в ближайшем будущем не придется перерабатывать существующие вычислительные методы и алгоритмы. Возможный выход состоит в разработке программ для некоторой идеальной системы, которая позволила бы описывать алгоритмы в машинно-независимой форме, адаптируемой к конкретной вычислительной среде с помощью систем программирования. Одним из вариантов такой независимости кода можно считать последовательное программирование, которое, на первый взгляд, выглядит весьма привлекательным, позволяя:
- применять опыт и продукты, накопленные в течение многолетней эксплуатации вычислительных машин с традиционной архитектурой;
- разрабатывать последовательные программы, не зависящие от особенностей параллельной вычислительной системы;
- не думать о параллельной организации программы, полагаясь в дальнейшем на то, что система автоматического распараллеливания решит все вопросы по эффективному переносу программ на любую параллельную систему.
В свое время этот подход достаточно широко и разносторонне исследовался. Однако многие из возлагаемых на него надежд не оправдались. ныне он практически не используется в промышленном программировании, так как обладает следующими недостатками:
- распараллеливание последовательных программ очень редко обеспечивает достижение приемлемого уровня параллелизма из-за ограничений вычислительного метода, выбранного для построения соответствующей программы, а выбор ограниченного метода часто обуславливается стереотипами последовательного мышления;
- в реальной жизни учесть особенности различных параллельных систем оказалось гораздо труднее, чем это изначально предполагалось.
Рассмотрим альтернативный подход – разработка параллельных программ, обладающих максимальным параллелизмом и не зависящих от ресурсных ограничений, определяемых числом процессоров, пропускной способностью каналов, размером оперативной памяти и т.д. Несмотря на то, что недостатки использования данного подхода уже были разобраны в работе [1], последнее слово здесь еще не сказано. Как один из вариантов его развития можно использовать сжатие максимального параллелизма с учетом налагаемых ресурсных и функциональных ограничений. Такой способ создания программ чем-то напоминает нисходящее программирование, однако, вместо постепенной детализации разрабатываемого алгоритма происходит аналогичное уточнение ограничений, накладываемых на параллелизм программы в соответствии со спецификой ее дальнейшего использования. В перспективе подобное «сжатие» можно проводить, опираясь на соответствующие инструментальные средства, однако программу можно преобразовать и «вручную».
Для демонстрации подхода рассмотрим сортировку элементов одномерного массива. Выбор задачи обусловлен широкой известностью, наличием множества вариантов решений, а также достаточно частой встречаемостью как в последовательных, так и в параллельных программах. Примерами разнообразного использования могут служить: сортировка списков контактов в органайзерах на персональных компьютерах и в мобильных телефонах, индексация таблиц баз данных в настольных и распределенных системах и т.д. Поэтому алгоритмы сортировки подвержены постоянному пересмотру и переписыванию в зависимости от используемого аппаратно-программного окружения.
Традиционный подход
На сегодняшний день предложено много приемов, повышающих скорость сортировки, причем впечатляет их эволюция, сопровождаемая постепенным накоплением эвристик [2]:
- сортировка с помощью прямого включения (Straight Insertion);
- сортировка методом деления пополам (Binary Insertion);
- сортировка с помощью прямого выбора (Straight Selection);
- сортировка с помощью прямого обмена (Bubble Sort);
- шейкерная сортировка (Shaker Sort);
- сортировка Шелла (Shell Sort);
- сортировка с помощью «дерева» (Heap Sort);
- сортировка с помощью разделения (Quick Sort);
- сортировка с помощью прямого слияния (Straight Merge).
Такое разнообразие затрудняет переход к параллельным реализациям. Нельзя сказать, что не существует эффективных решений, опирающихся на использование последовательных аналогов, но они зачастую касаются использования конкретных алгоритмов в конкретных условиях [3].
Сортировка перебором
Если абстрагироваться от эффективности вычислительного процесса и обратить внимание только на обеспечение максимально параллельной сортировки, то можно прийти к алгоритму, названному сортировкой перебором [3]:
- Каждый элемент Ai вектора A[0..n-1] сравнивается со всеми другими (включая и себя) с использованием отношения:
(Ai > Aj) или ((Ai = Aj) и (i > j)).
Все проверки проводятся одновременно.
- Для всех элементов вектора одновременно подсчитывается количество истинных результатов сравнения с формированием вектора сумм в соответствии с расположением элементов.
- Вектор сумм используется как набор индексов для одновременного размещения значений соответствующих ему элементов в новом векторе.
Пример, демонстрирующий использование данного алгоритма, приведен в таблице 1. Значения элементов вектора заимствованы из [2].
Анализ этого метода позволяет наложить на него некоторые ограничения, обеспечивающие переход к уже знакомым алгоритмам. При этом сжатие параллелизма обеспечивает также и «свертку» пространства возможных вариантов решений. Можно выделить:
- логические приемы, применяемые в том случае, если специфика самой задачи позволяет сократить количество выполняемых операций без ущерба для ее параллелизма;
- физические приемы, прямо или косвенно связанные с внесением ограничений на количество одновременно выполняемых операций (эти ограничения могут также определяться техническими характеристиками используемой параллельной системы).
Остановимся на некоторых вариантах (см. также www.softcraft.ru/parallel/maxsort/index.shtml).
Сокращение числа операций сравнения
Это логический прием, связанный с повышением эффективности использования ресурсов за счет удаления избыточных симметричных проверок, что возможно из-за специфики конкретной решаемой задачи. Уровень параллелизма алгоритма при этом не изменяется. В частности, для получения результата достаточно сравнить только пары операндов, расположенные в матрице отношений, представленной в таблице 1, выше главной диагонали. В этом случае количество проверок будет сопоставимым с их числом в простых последовательных алгоритмах (Straight Selection, Bubble Sort). Значения для отношений, определяемых главной диагональю, можно проставить без вычислений. Элементы, расположенные ниже главной диагонали, можно вычислить путем отрицания результатов, симметрично расположенных выше нее. В связи с тем, что для элементов, расположенных выше главной диагонали, i всегда будет больше j, условие можно свести к проверке отношения Ai>Aj. Индексы, используемые для перестановки элементов, можно получить еще проще – сложить единицы в строке некоторого операнда с его же нулями в столбце для отношений, расположенных выше главной диагонали. В этом случае вычисление отношений, расположенных ниже главной диагонали, проводить не нужно.
Существуют и другие варианты формирования нового местоположения элемента массива, например, его можно вычислять относительно текущей позиции. В этом случае индекс новой позиции формируется как сумма текущего положения и числа единиц по горизонтали, минус количество единиц по вертикали, на пересечении строки и столбца, для которых искомый элемент выступает в качестве первого и второго операнда одновременно (Таблица 2).
Таким образом, анализ исходной максимально параллельной формы зачастую позволяет сократить количество выполняемых операций без изменения уровня параллелизма алгоритма. Вместе с тем, для его переноса на реальную архитектуру необходимо учитывать ограниченность вычислительных ресурсов, что ведет к использованию разнообразных физических приемов.
Ограничение на количество сравниваемых первых операндов
Если за один шаг проводить сравнение только одного операнда со всеми остальными, то, вместо подсчета индекса можно перейти к неупорядоченному перераспределению элементов относительно текущего (Таблица 3). Позиция элемента увеличивается на число истинных результатов сравнения. Элементы меньше первого операнда размещаются слева от него без изменения порядка следования относительно друг друга. Элементы, больше, чем первый операнд, аналогичным образом размещаются справа.
Процесс сортировки рекурсивно повторяется, одновременно и асинхронно как для левой, так и для правой последовательности до тех пор, пока не будет получен окончательный результат. Таким образом, уменьшается число одновременно проводимых проверок, что ведет к снижению требований к вычислительным ресурсам, что особенно важно для портативных устройств. Полученный вариант относится к одной из разновидностей алгоритма быстрой сортировки. Для получения чисто последовательного варианта, соответствующего последовательной версии Quick Sort, достаточно перейти к последовательному сравнению элементов на каждом шаге.
Одновременное сравнение с соседними элементами
Еще большие ограничения накладываются, если допустить проверки элемента одномерного массива только с левым или правым соседом, что позволяет перейти к построению пузырьковых алгоритмов, в которых обмен данными осуществляется только между рассматриваемыми парами. Классическая схема получения результата с использованием одновременного сравнения всех соседних элементов описывается следующим образом: на нечетном шаге в качестве первых операндов используются элементы, стоящие на нечетном месте. На четном шаге б- наоборот. Для данных, используемых в качестве примера, результат будет получен после выполнения семи шагов:
Шаг 1: (44, 55), (12, 42), (94, 18), (06, 67) Б?? 44, 55, 12, 42, 18, 94, 06, 67
Шаг 2: 44, (55, 12), (42, 18), (94, 06), 67 Б?? 44, 12, 55, 18, 42, 06, 94, 67
Шаг 3: (44, 12), (55, 18), (42, 06), (94, 67) Б?? 12, 44, 18, 55, 06, 42, 67, 94
Шаг 4: 12, (44, 18), (55, 06), (42, 67), 94 Б?? 12, 18, 44, 06, 55, 42, 67, 94
Шаг 5: (12, 18), (44, 06), (55, 42), (67, 94) Б?? 12, 18, 06, 44, 42, 55, 67, 94
Шаг 6: 12, (18, 06), (44, 42), (55, 67), 94 Б?? 12, 06, 18, 42, 44, 55, 67, 94
Шаг 7: (12, 06), (18, 42), (44, 55), (67, 94) Б?? 12, 18, 06, 44, 42, 55, 67, 94
Скобками выделены пары, сравниваемые на каждом шаге.
Представленный способ можно ускорить, если осуществить одновременное сравнение каждого элемента массива с обоими соседями, а вместо перестановки пар осуществить обратную перестановку внутри непрерывной группы элементов, расположенных по убыванию. Ее характерной чертой является наличие непрерывной подцепочки истинных результатов. Следует отметить, что использование данного подхода ведет к увеличению числа сравнений на каждом шаге, но при этом уменьшается общее количество операций обмена данными. Использование алгоритма для уже приведенных данных позволяет получить результат за четыре шага:
Шаг 1: 44, 55, 12, 42, 94, 18, 06, 59 Б?? (44, 55), (55, 12),(12, 42), (42, 94), (94, 18), (18, 06), (06, 67) Б??
Переставить: 1-2, 4-6 Б?? 44, 12, 55, 42, 06, 18, 94, 67
Шаг 2: 44, 12, 55, 42, 06, 18, 94, 67 Б?? (44, 12), (12, 55), (55, 42), (42, 06), (06, 18), (18, 94), (94, 67) Б??
Переставить: 0-1, 2-4, 6-7 Б?? 12, 44, 06, 42, 55, 18, 67, 94
Шаг 3: 12, 44, 06, 42, 55, 18, 67, 94 Б?? (12, 44), (44, 06), (06, 42), (42, 55), (55, 18), (18, 67), (67, 94) Б??
Переставить: 1-2, 4-5 Б?? 12, 06, 44, 42, 18, 55, 67, 94
Шаг 4: 12, 06, 44, 42, 18, 55, 67, 94 Б?? (12, 06), (06, 44), (44, 42), (42, 18), (18, 55), (55, 67), (67, 94) Б??
Переставить: 0-1, 2-4 Б?? 06, 12, 18, 42, 44, 55, 67, 94
Эффективность способа особенно заметна, если все элементы отсортированы в обратном порядке. В этом случае достаточно одного шага сравнений и обмена. Подобный подход может использоваться и в последовательных алгоритмах для улучшения простой пузырьковой сортировки.
Сортировки слиянием
Предыдущий алгоритм позволяет прийти к выводу – внутри вектора формируются частичные подсписки с элементами, расположенными в порядке убывания или возрастания. Последние путем обмена легко сводятся к искомому отношению порядка, однако для двух соседних упорядоченных подсписков использование парных перестановок неэффективно, и в этом случае лучше применить слияние, которое также можно рассматривать как параллельный процесс и в общем случае можно реализовать как неограниченный алгоритм, аналогичный сортировке перебором:
- Каждый элемент первого упорядоченного подсписка проверяется на отношение «больше» («>») со всеми элементами второго упорядоченного подсписка. Все проверки проводятся одновременно. Подсписки могут быть разной длины.
- Для всех элементов первого подсписка одновременно подсчитывается количество истинных результатов сравнения, которые используются для смещения элементов вниз относительно своего текущего положения. Одновременно для всех элементов второго подсписка истинные результаты сравнения используются для подсчета смещений вверх.
- Формируется вектор индексов, используемый для одновременного размещения значений соответствующих ему элементов в новом векторе.
Пример использования этого алгоритма для двух упорядоченных векторов представлен в таблице 4.
Слияние перебором тоже может использоваться для построения алгоритмов с ограниченным параллелизмом по описанным ранее схемам.
Сама сортировка слиянием протекает как рекуррентный процесс, в котором на первом шаге отдельные соседние элементы одновременно сливаются в пары, затем пары сливаются в четверки и т.д. Можно показать, что для рассматриваемого набора данных она выполняется за три шага:
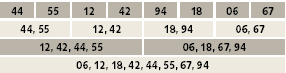
|
| Проверка отношения: Ai > Aj и слияние |
Заключение
Использование алгоритмов, описывающих максимальный параллелизм, предоставляет в распоряжение разработчика дополнительные методы анализа и построения ограниченных форм. Подход универсален и позволяет создавать не только параллельные, но и последовательные алгоритмы. Получаемые в результате программы могут рассматриваться как варианты использования, привязанные к определенной вычислительной среде.
В зависимости от неоднородности параллельной архитектуры можно использовать различные комбинации ограниченных алгоритмов, каждый из которых наиболее эффективно отображается на соответствующий уровень иерархии вычислительной системы. Допустимы также ограничения памяти, каналов ввода-вывода и др. Помимо этого, доказательство корректности максимально параллельного алгоритма и использование формальных преобразований при его сжатии позволяет автоматически переносить доказательство корректности и на окончательную версию, используемую для построения программы. n
Работа выполнена при поддержке РФФИ. Грант б№ 02-07-90135.
Литература
- Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. б- СПб.: БХВ-Петербург, 2002. б- 608 с.
- Вирт Н. Алгоритмы и структуры данных. – М.: Мир, 1989. б- 360 с.
- Grama A., Gupta A., Karypis G., Kumar V. Introduction to Parallel Computing, Second Edition. – Addison Wesley, 2003. 856 pp.
Александр Легалов (legalov@mail.ru) – профессор кафедры нейроЭВМ Красноярского государственного технического университета
