Немногие примеры их использования по-прежнему не выходят за рамки традиционных задач моделирования объектов, содержащих плавные сочленения, например ладони руки, деревья. Однако поверхности свертки способны на гораздо большее - морщины, складки, шипы, зубцы, шероховатости — все эти атрибуты, столь типичные для органических объектов и столь нетипичные для классических неявных поверхностей, можно достаточно просто построить с помощью поверхностей свертки.
Поверхности свертки - это интегральное представление неявно заданных поверхностей, известных в МГ как «капельные модели», «мета-сферы» или «мягкие объекты». Данные поверхности сочетают в себе гибкость капельных моделей и компактность «скелетных» методов, и представляют собой гораздо более мощное средство геометрического моделирования, чем традиционные модели неявных поверхностей.
Неявные модели и поверхности свертки
История использования неявно заданных поверхностей в машинной графике насчитывает уже почти два десятка лет: «капельные модели» (blobby model [1]), «мета-сферы» (metaballs [5]), «мягкие объекты» (soft objects [10]). Несмотря на различные названия, все эти модели описывают фактически один и тот же объект, а именно - изоповерхность S(p) уровня T в скалярном поле F(p):
Где поле F(p) задается в виде конечной суммы
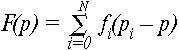 (2)
(2)
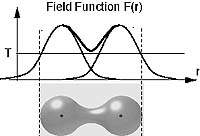 |
| Рис.1. Изоповерхность в поле двух точечных зарядов |
Каждый компонент fi(p) описывает поле точечного потенциала и обычно представлен какой-нибудь гладкой функцией, быстро затухающей с расстоянием от центра pi. Поверхности, представленные уравнениями (1) и (2), часто фигурируют под общим названием «классическая неявно заданная поверхность» или просто «блоб». Практические приемы и методы работы с неявными поверхностями во многом определяются их способностью к слиянию (типичный блоб показан на рис. 1). В результате, большинство объектов, заданных с помощью неявных поверхностей, содержат плавные сочленения (растения, тела людей и животных), либо демонстрируют некоторую «мягкость»: губы, лица, электронные облака в молекулах) или «текучесть» (кипящий суп) [2].
Поверхности свертки, которые были впервые применены в МГ Блюменталем и Шумейком в 1991 году ([3]), также являются изоповерхностями, с той разницей, что скалярное поле F(p) задается с помощью различных геометрических объектов. Если капельные модели («блобы»), построены из точечных компонентов-капель, то поверхности свертки базируются на более разнообразном выборе: точки, отрезки, дуги, треугольники и, в принципе, любые геометрические примитивы. Скалярное поле в таком случае вычсиляется с помощью интегрального оператора свертки двух функций
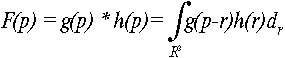 (3)
(3)
Фукнция g(p) описывает геометрию примитива, а функция h(p) называется ядром свертки и задает поле от точечного примитива. Пример свертки с отрезком показан на рис. 2, а более сложная поверхность изображена на рис. 3.
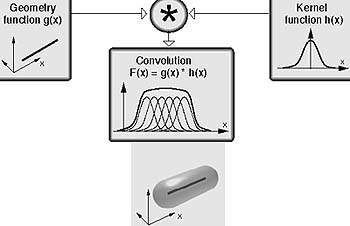 |
| Рис.2. Свертка с отрезком |
Как легко видеть из рис. 2 и 3, поверхности свертки объединяют в себе гибкость капельных моделей с возможностью использования примитивов различных форм и размеров. Если представить процесс моделирования как описание объекта на некоем геометрическом языке, то «словарный запас» большинства популярных моделей неявных поверхностей будет состоять из одного слова - точка. В языке поверхностей свертки набор слов-примитивов ограничен только воображением автора и, конечно, наличием программной реализации.
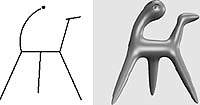 |
| Рис.3. Свертка с различными геометрическими примитивами: точка, отрезок, дуга. Прототипом этой модели является известная скульптура Деборы Харпет «Ангел» (Национальная Картинная Галерея, Мельбурн, Австралия) |
В определении поверхности свертки нет явных ограничений на геометрическую функцию g(p), и, в принципе, любой геометрический объект может быть использован как источник скалярного поля. На практике, выбор таких объектов жестко ограничен соображениями эффективности вычислений. До недавнего времени, только точечные и линейные примитивы позволяли найти аналитическое решение (3). Более сложные примитивы не поддавались интегрированию, что неизбежно влекло за собой использование косвенных методов. Как правило такие методы опирались на двух- и трехмерные сетки, заранее просчитанных значений поля, полученных численным интегрированием, с последующей интерполяцией между узлами. Нам же удалось получить аналитическое представление для геометрических примитивов пяти видов: точки, отрезка, дуги, треугольника и плоскости [6], что позволяет быстро считать изоповерхности F(x,y,z).
Система моделирования
Перечислим и кратно опишем основные понятия и методы, использованные в нашей системе геометрического моделирования RATS.
Неявные примитивы и скелетоны
 |
| Рис.4. Изоповерхности неявных примитивов: точка, отрезок, дуга, треугольник и плоскость (в паре с отрезком) |
Мы использовали пять различных скалярных функций f(p), полученных при помощи оператора свертки со следующими геометрическими примитивами: точка, отрезок, дуга, треугольник и плоскость. По аналогии с неявно заданными поверхностями, мы называем такие скалярные функции неявными примитивами. Каждая из этих функций при подстановке в уравнение (1) дает соответствующую изоповерхность (рис. 4).
Скелетон - это совокупность геометрических примитивов, которые вместе определяют общие очертания объекта. В терминах поверхностей свертки, скелетон задается суммой геометрических функций g(p). Оператор свертки обладает свойством линейности, что позволяет считать поле от всего скелетона по частям, а также строить сложные примитивы F(p) из простых компонентов. Например, из дуг можно легко строить кольца и спирали, из треугольников — многоугольники и так далее. Визуально скелетоны представляются геометрическим объединением примитивов, как показано на рис. 3 слева.
Материалы
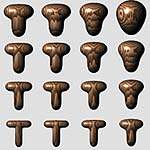 |
| Рис.5. Т-образная поверхность свертки. Увеличение липучести (слева направо) и собственного радиуса (снизу вверх) позволяет варьировать форму поверхности |
Как следует из приведенных уравнений, поверхность свертки задается скелетоном g(p), ядром h(p) и скалярным уровнем T. Скелетон при этом задает глобальную форму объекта, соответственно, локальные свойства поверхности должны определяться параметрами ядра h(p) и значением T.
В своей исторической работе [1] Блинн использовал функцию поля и два параметра, которые он назвал «собственным радиусом» R и «липучестью» B. Первый параметр задает размер сферы - изоповерхности от отдельно взятого точечного примитива (рис. 4, крайний слева). Второй параметр определяет насколько «охотно» примитивы слипаются вместе, когда оказываются рядом. Внешне это проявляется в толщине перемычки между примитивами (рис. 1).
Параметры R и B, введенные для точечной капельной модели (blobby model), можно легко перенести на более сложные примитивы, что мы и сделали для отрезков, дуг, треугольников и плоскостей. На рис. 5 показана серия Т-образных поверхностей с одним и тем же скелетоном и разными значениями R и B.
Удобно включить собственный радиус и липучесть в набор параметров, задающих оптические свойства поверхности, такие как цвет, коэффициенты преломления, отражения и так далее. Таким образом, мы расширили понятие материала, который помимо чисто фотометрических характеристик теперь еще несет и геометрическую информацию об объекте. Продолжая анатомическую аналогию со «скелетами», каждая «кость» (она же неявный примитив) оказывается покрытой своеобразной мягкой тканью с толщиной R и липучестью B, которую можно ассоциировать с эластичностью.
Профилирование
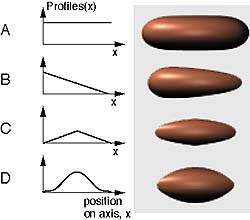 |
| Рис.6. Профилирование линейного отрезка |
Существует бесконечное число способов искажения «канонической» формы примитива, на рис.6 демонстрируется самый простой из них - умножение значения поля f(x,y,z) на различные «профилирующие» функции от аргумента x. Поскольку эти функции меняют значение поля, изоповерхности вынуждены следoвать этим изменениям.
Профилирующие функции могут быть заданы от двух и более переменных, включая время в анимации. Профилирование, являющееся чрезвычайно полезным расширением стандартной модели поверхностей свертки, в той или иной форме использовано во всех последующих примерах.
Офсетные поверхности
 |
| Рис.7. Простая спиральная модель морской раковины: офсетная поверхность (слева), неявная поверхность (справа). Число элементов: 361 |
Отдельно взятые неявные примитивы после визуализации очень похожи на свои собственные офсетные поверхности. А именно, точка превращается в сферу, отрезок — в цилиндр, закрытый двумя полусферами, дуга — в часть тора и т. д. Такое сходство подсказывает естественный способ ускорить процесс моделирования, заменив «настоящие» неявные примитивы их «двойниками» — офсетными поверхностями, которые легко поддаются визуализации, например, с помощью алгоритма трассировки лучей. Это позволяет легко манипулировать моделью, добавлять и убирать компоненты, менять их расположение; при этом каждая модификация отображается на экране (может быть, даже в реальном времени). Иначе говоря, офсетные поверхности - это удобные черновики, позволяющие быстро построить модель в первом приближении. Когда черновик готов, пользователь заменяет офсетные поверхности настоящими неявными примитивами, что включает такие тонкие эффекты, как слияние компонентов и профилирование - начинается тонкая настройка модели.
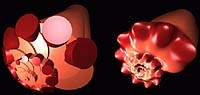 |
| Рис.8. Рогатая раковина, полученная наложением двух процедурных скелетонов. Число элементов: 70 |
В нашей системе моделирования и визуализации RATS мы поддержали такую двойственность, использовав расширенный синтаксис для всех неявных компонентов модели. Например командная строка «sphere Ice, r1, 0 0 -0.85» создает примитив, который может быть использован как обыкновенная сфера из заданного материала Ice, с радиусом r1 и центром в точке (0,0,-0.85). В таком режиме объект представляет собой офсетную поверхность. Если материал Ice содержит в списке своих параметров липучесть, то такая сфера в любой момент может принять «неявный» вид и. превратиться в точечную компоненту поверхности свертки. Для программы визуализации такое переключение задается простым флагом типа «да/нет». При этом перезагрузки модели в память не требуется, что особенно удобно для быстрого переключения между «явным» и «неявным» режимами визуализации.
Переменные параметры
Для большего удобства моделирования мы использовали переменные следующих типов: скаляр, вектор, цвет, материал и текстурa. В процессе работы с моделью переменные можно создавать и модифицировать «на лету». Благодаря использованию переменных, практически все параметры модели можно настроить в интерактивном режиме без перезагрузки модели в память. Эти параметры включают: геометрическое расположение скелетных элементов, их толщину и липучесть, все фотометрические характеристики материалов и текстур. Параметры камеры и источников света также можно задавать и настраивать с помощью переменных.
Практические примеры
 |
| Рис.9. Коралловое дерево. Ствол и ветви «выращены» процедурно, мелкие детали добавлены позже. Число элементов: 548 |
Приведем несколько практических примеров геометрического моделирования поверхностями свертки. Эти примеры сгруппированы вокруг соответствующих методов: глобальное задание формы объекта (скелетоны), локальные изменения (профилирование) и мелкие детали. Все скелетоны можно примерно разделить на четыре вида.
Процедурные скелетоны задаются алгоритмически и часто используются при моделировании самоповторяющихся структур: морские раковины, кораллы, деревья и другие «растущие» объекты. Модели на рис. 7 и 9, основаны на утилитах Эрика Хайнса [4].
 |
| Рис.10. Морской конек. Поверхность свертки собрана из 43 дуг, заданных вручную. Складки на хвосте и спине говорят о мягкости кожи |
Скелетоны «ручной работы». Пример такой модели приведен на рис. 10. Морской конек был изначально нарисован от руки на бумаге и продублирован в графическом редакторе набором дуг (слева). Дуги затем были превращены в офсетную поверхность (центр), а те, в свою очередь, — в поверхность свертки.
Скелетоны смешаннoго происхождения сочетают в себе процедурные и «самодельные» элементы. Скелетон рогатой раковины (рис. 8) получен с помощью процедурной модели круглой раковины (рис. 7) путем замены точечных элементов отрезками. Для этого достаточно добавить одну общую вершину, расположенную над плоскостью спирали, и соединить ее с центрами всех сфер. Подобным образом был получен второй набор отрезков («рога»); оба набора затем были прорежены и «слиты» в одну общую поверхность.
Импортированные скелетоны. Геометрическая модель Нефертити (сетка треугольников на рис. 12 слева) была использована в качестве скелетона поверхности свертки без каких-либо изменений.
Когда первый черновик модели готов (что соответствует офсетным поверхностям на левой стороне рис. 7-11), можно применять более тонкие методы работы с моделью. Как мы уже упоминали, одним из самых действенных приемов «обработки поверхности» является профилирование, во многом сходное с вырезанием формы из заготовки (рис. 6). Для аксиально симметричных заготовок-примитивов (например, цилиндров), профилирующие функции определяют поверхность вращения.
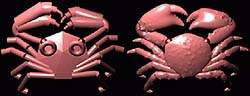 |
| Рис.11. Краб. Туловище, конечности и клешни смоделированные вручную (слева). Многочисленные неровности на всем панцире, а также зубцы на клешнях, добавлены с помощью утилит специального назначения. Число элементов: 641 |
Все элементы модели рогатой раковины (рис. 8) были профилированы синусоидальной функцией (рис. 6, внизу) - иначе фронт раковины превращался бы в одну аморфную массу. Подобным же образом были заострены зубцы клешней и конечные сегменты ног краба на рис. 11.
Реалистическое представление органических объектов требует очень высокой степени детализации их поверхности. Кроме того, чем больше деталей на поверхности, тем она интереснее для зрителя. Все типы деталей, использованные в системе RATS, можно примерно разделить на три группы:
Структурные детали создаются тривиальным добавлением большого числа мелких элементов. Добавочные элементы можно задавать вручную или с помощью специальных утилит. Примеры: коралловое дерево (рис.9), краб (рис. 11). Этот метод «грубой силы» может увеличить размер модели в десятки и сотни раз. Достоинства — простота реализации.
Функциональные детали — это профилирование отдельных примитивов с высокочастотными функциями. Пример — складки на хвосте и спине морского конька заданы с помощью функции t(x) = 1 + sin(x), где x - положение на дуге хвоста (спины) в радианах, параметры a и b задают глубину и частоту складок. Помимо элементарных профилирующих функций, можно использовать более интересные профили, например, двух- и трехмерный «шум», что может придать поверхности некоторую шероховатость. Заметим, что профилирующие функции лишь задают направление изменений в уровне изоповерхности, и конечный результат во многом зависит от влияния соседних компонентов модели. Если поле примитива (в данном случае дуги спины) невелико по отношению к вкладу соседей, то даже очень глубокие (a = 1) и даже отрицательные (a > 1) профили могут оcтаться незамеченными.
 |
| Рис.12. Нефертити, до (слева) и после свертки (центр, справа). Число элементов: 1242 |
Процедурные детали достигаются программными средствами. Пример —морщины на коже Нефертити (рис.12). Эта модель являет собой довольно необычный случай неявной поверхности. Сначала исходная сетка треугольников (рис. 12, слева) была превращена в поверхность свертки (рис. 12, центр), что вызвало значительные изменения в ее внешности - все тонкие черты полигональной поверхности оказались сглажены ядром свертки, работающим как фильтр низкой частоты. Чтобы уменьшить излишнюю размытость, поле от каждого треугольника было искусственно обрезано и затем плавно интерполировано эрмитным сплайном внутри. В итоге поверхность свертки оказалась буквально «прижатой» к сторонам треугольников, и приподнятой над их центральными областями. Внешний эффект — морщинистая поверхность (рис. 12, справа). Варьируя глубину морщин и толщину кожи (параметр R в описании материала), можно легко менять видимый возраст объекта.
Все описанные модели [9] были созданы в среде геометрического моделирования и визуализации RATS [7], написанной автором. Алгоритм трассировки лучей для неявных поверхностей описан в [8]. Офсетные поверхности также трассированы. В таблице 1 приведены времена визуализации некоторых моделей. Размер изображений 512 х 512 пикселей. Все изображения созданы в режиме повышенного качества, максимальное число первичных лучей - 16 на пиксель.
Заключение
Перефразируя известное высказывание, если единственным инструментом моделирования является точечный примитив-капля, то дизайнер вынужден смотреть на мир как на один огромный блоб. Многообразие форм и размеров примитивов устраняет такое неудобство и дает возможность применять неявные поверхности для решения широкого класса задач машинной графики. Реалистичное моделирование объектов органического происхождения - одно из них.
Об авторе
Андрей Шерстюк - научный сотрудник компании SquareUSA (Гонолулу, США) - ведущего производителя компьютерных игр и художественной анимации. Автор ряда статей в ведущих международных журналах по компьютерной графике. С ним можно связаться по электронной почте: andrei@squareusa.com
Литература
[1] J. Blinn, «A Generazation of Algebraic Surface Drawing», - ACM Transactions on Graphics, 1(3), 1982
[2] J. Bloomenthal (ed), «Introduction to Implicit Surfaces», - Morgan Kaufmann, 1997
[3] J. Bloomenthal and K. Shoumake, «Convolution Surfaces», - SIGGRAPH Proceedings, 1991
[4] E. Haines, «Standard Procedural Databases (SPD), ftp.princeton.edu:/pub/Graphics
[5] H.Nishimura et al, «Object Modeling by Distribution Function and a Method of Image Generation», - Transactions of the Institute Of Electronics and Communication Engineers of Japan, J68-D, 4, 1985
[6] J. McCormack and A. Sherstyuk, «Creating and rendering convolution surfaces», - Computer Graphics Forum, 17(2) 1998
[7] RATS Site: http://www.cs.monash.edu.au/~ash/rats/
[8] A. Sherstyuk, « Fast ray tracing of implicit surfaces, - Computer Graphics Forum, 1999, to appear
[9] A. Sherstyuk, - Interactive shape design with convolution surfaces, Proc. Of Shape Modeling International ?99, Aizu-Wakamatsu, Japan, March 1-4, 1999
[10] G. Wywill, C. McPheeters and B. Wywill, «Data Structure for Soft Objects», - The Visual Computer, 2(4), 1986
Русские идут с Востока
 |
| На снимке вместе со своими виртуальными «актерами»: Эрик Фаусетт, Валерий Аджиев и Александр Пасько (слева направо) |
Сегодня принято считать, что состояние компьютерной графики в России оставляет желать много лучшего и проходящие, несмотря ни на что, конференции «ГРАФИКОН» - это, скорее, исключение, подтверждающее правило. Однако бывает и на нашей улице праздник. Во всяком случае, становится очевидным, российская диаспора специалистов по МГ, работающих за пределами отчизны, процветает и задает тон мировому компьютерному сообществу. Подтверждением этому, например, можно считать итоги Международного конкурса «Dream Centenary - Computer Graphics Grand Prix 99» - самого престижного из проводимых в Японии фестивалей по компьютерному искусству, графике и анимации. Работы принимались по четырем номинациям: машинная графика, анимация, интерактивные и Web-приложения, художественные инсталляции. Всего в конкурсе участвовало 500 работ из 25 стран, в том числе более 200 - в анимационном разделе, который и оказался самым сильным: в первую шестерку награжденных вошли пять работ, непосредственно связанных с анимацией.
Во главу угла жюри ставило критерии научной и художественной оригинальности, отсеивая эффектные внешне работы, демонстрировавшие, однако, лишь более или менее изощренное владение известными методами и системами. Об уровне конкурса свидетельствует тот факт, что Главный Приз присужден анимационному фильму («Bunny») производства американской компании Blue Sky Productions. Эта история одиночества маленькой собачки, сделанная с использованием новых методов рендеринга на основе излучательности (radiosity), собрала все «золото» многих конкурсов и престижных фестивалей: выиграв Главный Приз на Imagina?98, работа была весной этого года удостоена премии «Оскар» за лучший анимационный фильм.
В этой связи весьма примечательно, в соперничестве с работами ряда известных профессиональных производителей, приз выиграл анимационный фильм «Homotopic Fun in 5D Space», среди трех авторов которого двое россиян и ассистент-американец. Призерами стали: доцент МИФИ Валерий Аджиев, профессор Университета Айзу Александр Пасько, ранее работавший в МИФИ, и студент Университета Айзу Эрик Фаусетт. Жюри по достоинству оценило оригинальную технологию генерации анимационной последовательности на основе функционально определенных многомерных геометрических объектов в сочетании с новым методом метаморфозиса. Успеху работы способствовала музыка Бориса Гребенщикова, сопровождавшая двухминутный фильм. Фильм был показан в программе мультимедийного шоу в рамках форума Eurographics?99 (Милан, Италия).
Аспирант кафедры «Кибернетики» МИФИ Анатолий Осипов стал победителем Международного Студенческого Конкурса-Форума по Мультимедийным технологиям, который проводился в рамках «взрослой» международной конференции «Распределенные Мультимедиа Системы» (DMS?99). На конкурс-форум в город Айзу-Вакамацу после проведенного международным жюри предварительного «заочного» отбора были приглашены 25 студентов и аспирантов из 7 стран. Российский аспирант Осипов получил главный приз (60 тыс. йен в денежном выражении) за презентацию статьи «Моделирование и визуализация многомерных геометрических форм в мультимедийных приложениях», поддержанную демонстрацией интерактивной системы многомерного моделирования «HyperFun for Windows».
Дмитрий Волков
| Модель | t1 | t2 | t1/t2 |
| Круглая раковина | 2:52 | 22:46 | 7:81 |
| Рогатая раковина | 12:54 | 41:16 | 3:20 |
| Морской конек | 5:25 | 11:52 | 2:19 |
| Краб | 14:03 | 46:13 | 3:29 |
