1. Обзор системы РООМА
2. Приложения
Заключение
Литература

Интерес к анимации в машинной графике последние годы неуклонно возрастает. Однако системы анимации весьма сложны в использовании, особенно при моделировании сцен, включающих большое количество объектов. Кроме того, большие трудности вызывает процесс создания сложных форм. В данной статье описывается основанная на физических принципах объектно-ориентированная система анимации РООМА (the Physically based Object Oriented Model Animator system), которая обеспечивает простой механизм анимации и лепки большого количества объектов. В системе РООМА используется концепция векторных полей как активных элементов, участвующих в процессах моделирования, лепки и анимации. В статье описываются архитектура, основные особенности системы РООМА, поддерживаемая ею иерархия классов геометрических объектов, а также приводятся конкретные примеры.

Анимация в машинной графике играет важную роль в областях, связанных со сферой развлечений, визуализацией данных и процессов, равно как и во многих других приложениях, где возникает необходимость интерактивного динамического изменения объектов во времени. Сегодня разработано немало систем, обеспечивающих автоматизированные средства для создания компьютерных анимаций. Описание наиболее известных из них можно найти в работах [3,4,6,13]. Одной из основных проблем, возникающих при использовании традиционных систем анимации, является сложность одновременного моделирования большого числа объектов. Другая трудность связана со сложностью интерактивного изменения объектов в сцене.

Основанная на физических принципах объектно-ориентированная система анимации РООМА предоставляет пользователю высокоуровневые средства интерактивного управления средой моделирования. С помощью этих средств художник или дизайнер может с минимальными усилиями быстро создавать или модифицировать мультфильмы, а также формировать и редактировать широкий круг моделей. При реализации системы РООМА использован комбинированный подход, объединяющий в себе анимационные методы, физические принципы и векторные поля. Он обеспечивает простые и удобные интерактивные средства анимации сложных сцен, включающих большое количество объектов.

Раньше векторные поля использовались только как пассивные объекты, которые являлись предметом визуализации и изучения. Разрабатывались различные технологии для визуализации векторных полей, в том числе метод траекторий [12], потоковых объемов [7], многоугольников течений [10], плоских и конических стрелок [8] и имиджей [2]. В системе POOMA векторные поля играют активную роль, они являются не только предметом визуализации, но и средством манипулирования изображаемыми объектами. Связанные интерактивные векторные поля обеспечивают понятный и удобный в использовании механизм управления объектами в среде моделирования. Они обеспечивают пользователю гибкие средства интерактивного взаимодействия с системами частиц, мягкими пластичными объектами, а также средства формирования скульптурных поверхностей по наборам трехмерных данных в моделируемом пространстве.

При использовании традиционных методов для реалистичной анимации систем, содержащих сотни частиц, задача генерации и описания поведения отдельных частиц становится весьма обременительной. Интерактивные векторные поля предоставляют потребителю средства глобального контроля, которые позволяют в интерактивном режиме манипулировать большими системами частиц и моделировать такие эффекты, как взрывы, коллапсы и разрушения. Кроме того, интерактивные векторные поля могут применяться и для локального контроля. Путем регулирования размеров векторных полей можно задавать гранулированность поверхностей и редактировать зернистые объекты. При редактировании трехмерных данных с помощью векторных полей имеется возможность эмулировать такие инструменты, как отбойные молотки, дрели и циркулярные пилы. Векторные поля применяются также для задания формы пластичных тел и описания их движения при моделировании различных визуальных эффектов.

1. Обзор системы РООМА

Система анимации POOMA построена на основе инструментальных средств SGI Inventor. Общая структура РООМА показана на рис.1.

Компонент среды моделирования предназначен для управления динамикой объектов на основе физических закономерностей и содержит интерактивные векторные поля и другие объекты системы. В нем же осуществляется расчет динамики объектов. Второй компонент обрабатывает инициируемые пользователем события и поддерживает интерактивное взаимодействие с объектами среды. Компонент рендеринга осуществляет визуальную обратную связь, так что изображения объектов среды всегда доступны пользователю. Компоненты рендеринга и обработки событий поддерживаются средствами Inventor.

Рисунок 1.
Общая структура системы РООМА.

1.1 Среда моделирования

Компонент среды моделирования РООМА содержит объекты и векторные поля. Кроме того, в нем выполняются все вычисления, связанные с расчетом динамики и кинематики объектов. Основные функции компонента среды моделирования следующие: обеспечение механизма прерываний по времени для вычислительных циклов моделирования; расчет кинематики и динамики на основе физических закономерностей; своевременная передача управления и данных библиотеке Inventor для обработки событий и выполнения рендеринга.

В рамках компонента среды моделирования имеется один главный узел, называемый Директором (Director), и несколько дочерних узлов моделирования (Simulation Environment). Узлы моделирования могут содержать векторные поля, системы частиц, мягкие пластичные объекты, а также модели данных. Главный узел начинает цикл моделирования с обратными вызовами прерываний по времени в процессе инициализации системы. Затем каждый узел моделирования выполняется независимо от других узлов данного уровня. Независимость узлов моделирования обеспечивает сосуществование нескольких моделируемых процессов в системе.

Для каждого узла моделирования выполняемые в нем физические вычисления разбиваются на три шага. На первом шаге рассчитываются перемещения объектов в соответствии с текущими значениями их скоростей, ускорений и моментов. На втором шаге область действия каждого векторного поля сравнивается с ограничивающими объемами объектов и выделяются те объекты, которые попадают в область влияния этого поля. Далее рассчитываются порождаемые данным векторным полем силы, приложенные к различным частям выделенных объектов. Наконец, на третьем шаге для каждого объекта определяются равнодействующие всех сил, порождаемых векторными полями, с учетом этих сил вычисляются новые значения скорости, ускорения и моментов для следующего временного слоя.

После того как заканчивается расчет взаимодействия объектов и полей на очередном временном слое, управление передается средствам Inventor для выполнения рендеринга и обработки очереди сообщений. Затем при возникновении нового прерывания по времени главный узел начинает выполнение следующего цикла вычислений. Расчеты по данной схеме продолжаются до тех пор, пока их не остановит пользователь. Для инициирования процесса моделирования пользователю достаточно только указать позиции объектов сцены и задать положения и направления действия векторных полей. Пользователь имеет возможность интерактивного взаимодействия со сценой, он может перемещать векторные поля, сдвигать и вращать объекты, изменять точку наблюдения и т. д. С началом процесса моделирования все объекты начинают двигаться в соответствии с приложенными к ним силами.

Управление средой моделирования в системе РООМА осуществляется с помощью механизма квантования по времени, который позволяет распределять время между тремя областями: областью вычислений, областью взаимодействия с пользователем и областью рендеринга. Для регулирования временных квантов в этих областях используются прерывания. По прерыванию от таймера запускается очередной цикл обработки модели. В процессе обработки проводятся физические расчеты в узлах моделирования в соответствии с выделенным временным интервалом.

Одна из проблем, которая при этом возникает, связана с тем, что центральный процессор может быть настолько занят физическими расчетами, что пользовательские сообщения останутся необработанными. С другой стороны, если сообщениям, поступающим от устройств ввода, дать слишком высокий приоритет, то не будут доведены до конца физические вычисления. Мы решили эту проблему с помощью метода динамических временных окон (Dynamic Time Windows). Основная идея метода заключается в использовании знаний о времени вычислений на предыдущем этапе для определения временного интервала, выделяемого для расчета текущего шага. Если время вычислений уравнений движений возрастает, то увеличивается и время, выделяемое области вычислений, но не за счет исключения области обработки сообщений. Если мы представим распределение процессорного времени как множество окон в смысле доступа к CPU, то каждому такому окну в системе моделирования можно дать свое специфическое название. Процессу обработки сообщений, поступающих от устройств ввода, мы поставили в соответствие временное окно, получившее название окна пользовательских событий (UETW - User Event Time Window). Анализ пересечений и расчет уравнений движения занимает временной интервал, который мы назвали окном вычислений (CTW - Calculation Time Window). Наконец, поскольку рендеринг модели обеспечивает обратную связь, соответствующее временное окно получило название окна обратной связи (FTW - Feedback Time Window).

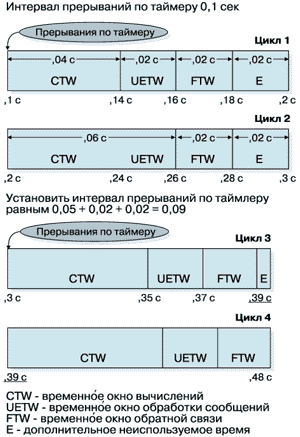
Рисунок 2.
Динамические временные окна.

На рис. 2 приведен пример, подтверждающий, что применение динамических временных окон позволяет рационально использовать время процессорного цикла, обеспечивая при этом гарантированную возможность интерактивного взаимодействия с системой. После выполнения первых двух циклов моделирования, время вычислений в которых составило соответственно 0,04 и 0,06 с., был рассчитан новый временной интервал для окна CTW, он был получен как среднее арифметическое интервалов предыдущих циклов и составил 0,05 с. Общее время моделирования складывается из времени вычислений (0,05с.), времени обработки событий (0,02с.) и времени рендеринга (0,02с.), для третьего цикла оно составило 0,09 с. Было установлено новое значение интервала прерываний, по времени равное 0,09 с. Описанный подход позволяет обрабатывать сообщения от устройств ввода, не накапливая их в очереди, и в то же время обеспечивает рациональное использование ресурсов CPU.

В методе динамических временных окон прерывания по таймеру включаются через равные промежутки времени, устанавливаемые пользователем (например, через 0,1 с.). При возникновении прерывания осуществляется вызов главного узла. Главный узел сначала проверяет время, а затем запускает вычисления. После завершения вычислений время, затраченное на их проведение, запоминается. Затем в течение заданного интервала идет обработка очереди сообщений и выполняется рендеринг. Поскольку размер окна вычислений не может превысить интервала между соседними прерываниями по времени, процесс моделирования остается интерактивным, хотя при этом часть времени процессорного цикла, которая могла бы пойти на проведение вычислений, может оказаться неиспользованной.

В РООМА при моделировании систем, включающих большое число частиц, время вычислений может значительно возрасти при вводе в рассмотрение векторного поля. Размер окна CTW существенно увеличивается также при росте числа векторных полей в пространстве моделирования. Если допустить, что размеры окна CTW будут в несколько раз превосходить интервал переключения, прерывание или размеры окна UETW, то сообщения, поступающие от внешних устройств, и события, связанные с прерываниями по времени, будут накапливаться в очереди и останутся необработанными. Таким образом система сама переведет себя в неинтерактивный режим. Во избежание подобной ситуации главный узел разбивает время вычислений на несколько частей, количество которых определяется пользователем. Интервал прерываний по времени устанавливается в соответствии с уменьшенным размером окна CTW. Это дает системе возможность обрабатывать очередь сообщений на каждом цикле вычислений. Такой подход способствует достижению сразу двух целей. Он обеспечивает время для расчета уравнений движения и в то же время позволяет выделить время для обработки сообщений от внешних устройств. Таким образом, вычислительный процесс и процесс обработки событий существуют в системе одновременно и ни один из них не захватывает все процессорное время.

1.2 Иерархия классов

На рис. 3 представлена иерархия основных классов РООМА. Стрелки, направленные сверху вниз, показывают, что классы более низкого уровня (подклассы) наследуют функциональные возможности классов более высокого уровня (суперклассов).

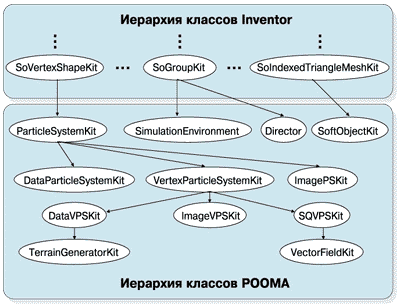
Рисунок 3.
Иерархия классов объектов системы РООМА.

Inventor обеспечивает иерархию базовых геометрических классов, таких как SoVertexShapeKit и SoIndexTriangleMeshKit. Кроме того, он поддерживает класс иерархического группирования, называемый SoGroupKit. Эти три класса составляют основу для конструирования объектов и разработки геометрии для РООМА. Указанные классы также содержат методы, которые обеспечивают выполнение рендеринга и поддерживают реализацию функций указания геометрических элементов с помощью устройств ввода. Когда на базе перечисленных выше классов создаются новые подклассы, Inventor обеспечивает наследование таких функций, как выбор, копирование и вставка. Таким образом, иерархия классов РООМА наследует у Inventor функциональные возможности указания, выбора, копирования, вставки и удаления. Кроме того, РООМА обеспечивает свои собственные интерактивные средства, основанные на физических принципах, а также поддерживает широкий набор объектов, которые могут быть использованы для разработки различных приложений.

РООМА поддерживает базовый класс систем частиц ParticleSystemKit и соответствующие ему подклассы (рис. 3). Класс ParticleSystemKit содержит все функции, необходимые для семейства классов частиц. Каждая частица в системе имеет центр масс, скорость, ускорение и позицию для расчета простых перемещений. Частица по умолчанию является плоским треугольником.

Класс DataParticleSystemKit наследует все свойства класса ParticleSystemKit, но использует для задания систем частиц трехмерные модели данных. Каждый многоугольник в модели данных разбивается на треугольники в соответствии с заданным пользователем максимальным радиусом описанной окружности для треугольников. Каждая частица имеет также приписанную ей массу. В этом случае динамика движения для заданного набора данных хорошо описывается моделью жесткой системы частиц. Данные могут также обрабатываться как системы частиц при моделировании эффектов взрывов и разрушений.

VertexarticleSystemKit - это абстрактный класс, который наследует все свойства класса ParticleSystemKit. Этот класс рассматривает вершины индексной треугольной сетки в качестве частиц. При определении сетки пользователь может задавать ее размер и плотность. Сетка формируется таким образом, чтобы все ее вершины являлись компланарными. Поскольку движение вершин сетки описывается динамикой соответствующей системы частиц, то треугольники сетки в процессе движения остаются связанными.

ImagePSKit - это еще один подкласс класса ParticleSystemKit. Он позволяет задавать системы частиц по изображениям. Каждому пикселу изображения ставится в соответствие своя частица. Для пикселов строятся прямоугольники, центры которых задают положение соответствующей частицы. Любые изображения произвольных размеров допустимы в качестве исходных данных для данного класса.

Класс DataVPSKit наследует геометрические и физические свойства системы частиц класса VertexParticleSystemKit. Однако для задания системы частиц он допускает использование произвольных индексных треугольных сеток.

Класс TerrainGeneratorKit является подклассом DataVPSKit. В качестве исходных данных для генерации системы он может использовать либо произвольную, заранее построенную треугольную сетку, либо сформированную с помощью средств класса стандартную плоскую сетку. По сравнению с DataVPSKit этот класс предоставляет дополнительную возможность получения цветного изображения треугольной сетки, в котором цвет, плавно меняющийся в пределах заданной пользователем палитры, для каждой отдельной точки определяется в зависимости от ее высоты. В процессе моделирования высота вершин динамически изменяется, при этом осуществляется автоматическое обновление раскраски сетки. С помощью этого класса можно описывать рельеф местности, а также моделировать и другие объекты, для которых удобно рассматривать цвет как функцию высоты.

Класс ImageVPSKit является подклассом класса VertexParticleSystemKit и наследует его функциональные возможности работы с индексными треугольными сетками и соответствующими им системами частиц. Класс ImageVPSKit аналогичен классу ImagePSKit за исключением того, что цвет пикселов изображения используется в нем для раскраски индексной треугольной сетки. Исходное изображение задается при инициализации объекта данного класса. В соответствии с размером изображения формируется треугольная сетка. Цвет вершин сетки определяется по цвету соответствующих им пикселов изображения. Данный класс может использоваться для восстановления рельефа местности по фотографиям и снимкам, а также для построения любых других трехмерных поверхностей по их двухмерным отображениям.

Класс SQVPSkit предназначен для моделирования квадратичных поверхностей. Он наследует свойства класса VertexParticleSystemKit. Квадратичная геометрия задается на индексной треугольной сетке. Вершины сетки определяют положение соответствующих им частиц. В отличие от других подклассов VertexParticleSystemKit в классе SQVPSkit сетка является замкнутой и связной. Данный класс поддерживает эллипсоиды и торроиды. Параметры объектов указанных типов задаются пользователем.

Класс VectorFieldKit разработан как подкласс класса SQVPSKit. Для своих объектов он обеспечивает функциональные возможности аналогичные возможностям жестких систем частиц и квадратичных поверхностей, заданных на индексной треугольной сетке. Кроме того, он включает дополнительные методы, реализующие специфические для векторных полей функции. При разрешении коллизий и расчете точечных преобразований векторные поля сами по себе могут рассматриваться как жесткие тела, способные сталкиваться с жесткими телами, соответствующими другим векторным полям, а также оказывать влияние на мягкие пластичные тела и системы частиц.

Класс SoftObjectKit используется для задания мягких, пластичных тел. Эти тела могут деформироваться, изгибаться, растягиваться, сжиматься и вибрировать в соответствии с приложенной к ним силой. Для описания поведения пластичных тел используется модель, предложенная в работе [9]. Движение и форма этих тел рассчитываются на основе метода конечных элементов и методов оптимизации [1]. Каждое тело описывается 27-узловым конечным элементом. Силы, действующие на тело, прикладываются к этим узлам - результирующая определяет изменение формы тела.

1.3 Воздействие векторных полей на объекты

Векторные поля одинаковым образом воздействуют на различные объекты. Благодаря полиморфизму методов в языке программирования С++ для каждого объекта рассчитывается соответствующая ему реакция на воздействие векторных полей. В цикле вычислений узел моделирования рассчитывает влияние векторного поля на объекты путем вызова метода ApplyVectorField для каждого объекта. После обработки всех векторных полей узел моделирования вызывает для каждого объекта метод ResolveLoad для расчета реакции на результирующие нагрузки. Этот метод приводит к вычислению уравнений конечных элементов и оптимизации для пластичных тел, определению перемещений частиц для систем частиц и расчету динамики жестких тел.

Вдобавок следует отметить, что каждая такая система имеет флаг состояния, который указывает, является ли данная система жесткой или свободной. В первом случае система рассматривается как единый объект, который движется как жесткое тело. Во втором - каждая частица перемещается независимо от других в соответствии со своими собственными уравнениями движения.

Поскольку векторные поля являются подклассами класса систем частиц, они также имеют флаг состояния. Использование этого флага позволяет в процессе анимации изменять статус объектов, попадающих в сферу влияния поля. Например, в начале процесса моделирования некоторая система частиц может быть жестким телом, затем, попав в поле с соответствующим значением флага состояния, она распадается на множество несвязанных частей, каждая из которых может двигаться в своем направлении и со своей скоростью. Кроме того, векторные поля имеют флаг с указанием времени действия поля. Это дает пользователям возможность в процессе анимации включать и выключать отдельные поля, создавая разнообразные эффекты.

2. Приложения

Рассмотрим различные приложения, которые были разработаны для оценки эффективности и гибкости РООМА, использующей векторные поля в качестве средств интерактивного взаимодействия пользователя с элементами сцены. Примеры применения РООМА в области анимации и моделирования в различных прикладных областях иллюстрируют возможности адаптации системы и настройки ее на решение разнообразных типов задач. Другие приложения РООМА, связанные с использованием векторных полей при анимации жестких и пластичных тел и моделировании таких эффектов, как разрушения, взрывы и т. д., описаны в работе [5].

2.1 Построение трехмерных рельефов по двухмерным изображениям

а
б
с
Рисунок 4.
Формирование рельефа по плоскому изображению с использованием индексной треугольной сетки и векторного поля.

Построение трехмерных рельефов по двухмерным изображениям - это одно из приложений, которое легко реализуется с помощью интерактивных векторных полей. Индексная треугольная сетка образует основу формирования поверхности рельефа. На рис. 4 показана одна из таких сеток, раскрашенная в соответствии с заданным изображением. В данном примере изображение 50х50 пикселов было передано на индексную треугольную сетку 50х50 вершин. На рис. 4а показано векторное поле, направленное по нормали к исходной сеточной поверхности, которое использовалось для изменения высоты вершин сетки. В интерактивном режиме задавалось перемещение этого поля по сетке. Полученные в результате поверхности, представлены на рис. 4в и рис. 4с. Чем дольше задерживалось поле в некоторой точке, тем больше была высота вершин сетки в этом месте. Естественное приложение описанной методики - это построение трехмерных рельефов по плоским фотографиям.

2.2 Формирование цветных рельефов

На рис. 5 показан еще один пример моделирования рельефа. По сравнению с предыдущим здесь добавлены средства динамической раскраски вершин сетки в соответствии с цветовой картой высот, устанавливающей связь между высотой и цветом. На рис. 5а представлена исходная плоская индексная треугольная сетка, моделирующая океан, вершины сетки окрашены в голубой цвет, соответствующий уровню моря. Векторное поле направлено по нормали к поверхности океана. При перемещении поля изменяется высота вершин. По мере роста высоты вершины окрашиваются в зеленый, коричневый, желтый и, наконец, белый и серый цвета, соответствующие вершинам гор. Долины и впадины могут быть получены с использованием векторных полей, которые направлены внутрь сетки. Горная гряда (рис. 5в) была построена в интерактивном режиме всего за две минуты. Задавая различную плотность сетки, можно изменять разрешение, с которым формируется рельеф.
а
б
Рисунок 5.
Формирование рельефа с помощью цветной индексной треугольной сетки, цветовой палитры высот и векторных полей.

Помимо построения рельефов, описанная методика может применяться для решения любых других задач, в которых требуется двухмерное изображение растянуть вдоль третьего измерения.

2.3 Формирование скульптурных поверхностей

Рисунок 6.
Формирование скульптурной
поверхности с помощью векторных
полей.
Процесс лепки может быть смоделирован путем изменения поверхности объекта, описываемой индексной треугольной сеткой. При этом могут использоваться, в частности, и замкнутые сетки. Так, на рис. 6а показано яйцевидное тело, поверхностная сетка которого построена по данным решения неявного уравнения поверхности. Векторные поля были использованы для имитации вдавливания поверхности, в результате было получено тело в форме челнока Так как объект описывается треугольной сеткой, его связность в процессе моделирования не изменяется. Отдельные порции поверхности можно вдавливать внутрь или вытягивать наружу, однако образование дыр в поверхности недопустимо.

 

 

2.4 Специальные визуальные эффекты

Используя системы частиц, можно создавать различные визуальные эффекты. Один из таких примеров приведен на рис. 7, где изображение 50х50 пикселов (рис.7а), преобразуется в систему частиц. Каждому пикселу ставится в соответствие цветной четырехугольник. На рис. 7в показаны два векторных поля, которые используются для создания эффектов. Одно из них представляет собой торроидальное поле с направлением векторов против часовой стрелки, а второе - цилиндрическое поле, с направлением векторов по часовой стрелке. В процессе моделирования одни частицы разлетаются по часовой стрелке, другие в противоположном направлении. Полученные таким образом анимации могут найти применение в областях, связанных с рекламой и индустрией развлечений.
а
б
Рисунок 7.
Спецэффекты, полученные с помощью векторных полей.

2.5 Другие возможные приложения

Существует целый ряд различных приложений, которые легко могут быть добавлены к системе. Некоторые из них включают автоматическое раскрашивание ландшафтов, обеспечивающее более реалистичное изображение. Векторные поля могут применяться для создания эффекта снежных бурь при изменяющейся во времени заливке белым цветом вершин сетки. Скорость заливки и плотность наложения цвета зависят от числа вершин и могут быть уставлены либо пользователем в интерактивном режиме, либо с помощью специально выбранных функций. Векторные поля могут также использоваться для поиска в сетке фрагментов, отличающихся особенностью или неоднородностью геометрии. В этих местах с помощью векторных полей можно закрасить вершины сетки зеленым цветом для имитации перевалов и долин. Кроме раскрашивания ландшафтов, векторные поля могут быть использованы со специальными приложениями для моделирования течения жидкости, воздушных вихрей, а также рек. Пользователь может добавить эти средства в анимационные системы для включения таких динамических объектов в сложную анимацию. Они являются прекрасным инструментом при создании рекламы, мультипликации, а также в научном моделировании.

Заключение

В статье дано описание POOMA - объектно-ориентированной трехмерной системы для анимации, формирования сложных поверхностей и моделирования. Для этой системы были разработаны и внедрены алгоритмы имитационного моделирования, динамики пластичных объектов, динамики жестких и свободных систем частиц, а также взаимодействия векторных полей. Кроме того, была создана иерархия классов, включающая классы, основанные на системах частиц и пластичных объектах. В статье представлены несколько приложений, которые показывают, что интерактивные средства работы с векторными полями вместе с различными типами геометрии обеспечивают гибкий механизм и инструменты контроля для дизайнеров и специалистов по моделированию. В отличие от существующих в этой системе средств общие и локальные средства управления объектами представлены в виде единого интерактивного инструмента. Авторы не утверждают, что инструментарий векторных полей заменит сценарии и другие традиционные средства анимации, но полагают, что существенно дополнит их.

Система POOMA была разработана на графической станции SGI Indigo, которая позволила проводить интерактивные расчеты в цикле по 4.0 с для систем из 30 500 частиц. Также было установлено, что для 10 векторных полей и 10 пластичных объектов полный цикл пересчета состояния составляет 4,66 с. Эти факты позволяют сделать вывод, что в ближайшем будущем такие средства дадут возможность широкому кругу пользователей заниматься интерактивным моделированием и анимацией больших систем частиц и пластических объектов на обычных настольных системах.

Литература

  1. K. Bathe, Finite Element Procedures in Engineering Analysis,Englewood Cliffs, NJ, Prentice-Hall, 1982.
  2. B. Cabral, L. Leedom, "Imaging Vector Fields Using Line Integral Convolution," Computer Graphics, Annual Conference Series, ACM SIGGRAPH, Anaheim, California, pp. 263-270, (1993).
  3. P. Getto, D. Breen, "An Object-Oriented Architecture for a Computer Animation System," Visual Computer, Vol. 6, No. 2, pp. 79-92, March 1990.
  4. J. E. Gomez, "Twixt: A 3D Animation System," EUROGRAPHICS '84, Elsevier Science Publishers B. V. (North-Holland), Copenhagen, Denmark, pp. 121-133, (12-14 September, 1984).
  5. T. L. Hilton, P. K. Egbert, "Vector Fields: an Interactive Tool for Animation, Modeling and Simulation with Physically Based 3D Particle Systems and Soft Objects," Proceedings of Eurographics 94, Computer Graphics Forum, Vol. 13, #. 3, pp. 329-338, 1994.
  6. N. W. John, P. J. Willis, "The Controller Animation System," Computer Graphics Forum, Vol. 8, No. 2, pp. 133-138, June 1989.
  7. N. Max, B. Becker, R. Crawfis, "Flow Volumes for Interactive Vector Field Visualization," Visualization '93, IEEE Computer Society Press, San Jose, California, pp. 19-24, (1993).
  8. N. Nassif, P. P. Silvester, "Graphic Representations of Three-Component Vector Fields," Computer-Aided Design, Vol. 12, #. 6, pp. 289-294, November 1980.
  9. A. Pentland, S. Sclaroff, "Closed-Form Solutions for Physically-Based Modeling and Recognition," IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 13, No. 7, pp. 715-729, July 1991.
  10. W. J. Schroeder, C. R. Volpe, W. E. Lorensen, "The Stream Polygon: A Technique for 3D Vector Field Visualization," Visualization '91, IEEE Computer Society Press, San Diego, California, pp. 126-132, (October 22-25, 1991).
  11. P. S. Strauss, R. Carey, "An Object-Oriented 3D Graphics Toolkit," Computer Graphics (SIGGRAPH '92 Conference Proceedings), Vol. 26, #. 2, pp. 341-349, July, 1992.
  12. R. B. Wilhelmson, B. F. Jewett, C. Shaw, L. J. Wicker, M. Arrott, C. B. Bushell, M. Bajuk, J. Thingvold, J. B. Yost, "A Study of the Evolution of a Numerically Modeled Severe Storm," The International Journal of Supercomputer Applications, Vol. 4, #. 2, pp. 20-36, Summer 1990.
  13. R. C. Zeleznik, D. B. Conner, M. M. Wloka, D. G. Aliaga, H. T. Huang, P. M. Hubbard, B. Knep, H. Kaufman, J. F. Hughes, A. v. Dam, "An Object-Oriented Framework for the Integration of Interactive Animation Techniques," Computer Graphics (SIGGRAPH '91 Conference Proceedings), Vol. 25, #. 4, pp. 105-112, July 1991.
  14. Е. Валентинов. Open Inventor как средство разработки интерактивных графических приложений. Открытые системы 1997, # 6(26).