При обработке любой сколь-нибудь значимой информации с помощью отдельного компьютера, а тем более в сети, возникает вопрос о ее защите от несанкционированного доступа и использования. Наиболее распространенный в компьютерных системах способ защиты - использование паролей - более пригоден для защиты доступа к вычислительным ресурсам нежели для защиты информации. Это своеобразный забор, отгораживающий законных пользователей системы от посторонних, пройдя сквозь который, квалифицированный программист получает доступ практически ко всей информации.
"Классическая" криптозащита
Другой способ защитить наиболее важную и чувствительную информацию - хранить и передавать ее только в зашифрованном виде. В этом случае она оказывается "запертой в надежном криптографическом сейфе", ключ от которого хранится только у его хозяина. Такой способ позволяет гораздо надежнее защитить информацию, но создает и некоторые новые проблемы.
Первая из них - создание общепризнанного надежного алгоритма шифрования - разрешилась в определенной мере принятием в 1973 году в США первого открытого стандарта на шифрование данных (алгоритм DES), который затем проходил аттестацию в 1978, 1982, 1988 и 1992 годах, претерпев лишь ряд непринципиальных изменений. По аналогии с алгоритмом DES в ряде стран были также приняты стандарты на шифрование информации (алгоритм FEAL-8 в Японии в 1988 году, алгоритм ГОСТ 28147-89 в СССР в 1989 и т. д.) Это в основном позволило ответить на вопрос о том, как надо шифровать информацию.
Главная же проблема, возникающая при использовании криптографических методов защиты информации, - это работа с ключами для шифрования/расшифрования.
Сами современные алгоритмы шифрования строятся так, что их знание не может заметно помочь в раскрытии зашифрованной информации, если остается неизвестным единственный (ключевой) элемент шифра, обычно так и называющийся - ключ. В традиционной системе криптографической защиты информации для зашифрования и расшифрования используется один и тот же ключ, сохранение которого в секрете обеспечивает надежность защиты. Обычно в качестве такого секретного ключа выступает некоторая последовательность символов (цифр, букв...).
Ключ не может быть слишком коротким, так как в этом случае его можно будет определить, перебирая все возможные варианты и пытаясь расшифровать информацию. Но он не может быть и слишком длинным, бессмысленным набором символов, если иметь в виду его запоминание пользователем (набор из 7 цифр телефонного номера люди в подавляющем большинстве предпочтут записать на бумаге). Поэтому секретные ключи для шифрования/расшифрования информации обычно записываются на специальные носители и хранятся с наибольшей возможной надежностью.
Кроме того, секретный ключ для шифрования имеет особенность со временем терять свое главное качество - обеспечивать пользователю уверенность в надежности защиты информации. Действительно, если Вы пользуетесь для шифрования наиболее важных файлов одним ключом в течение пяти лет и при этом храните файлы в общедоступной области памяти, снятие копии с Вашего ключа даст возможность злоумышленнику пользоваться этой информацией в течение всего срока действия ключа.
Поэтому ключи для шифрования желательно по возможности чаще менять.
Если Вы пользуетесь своими ключами для шифрования только сами, то в этом нет особой проблемы, кроме необходимости соблюдать некоторую аккуратность при смене ключей, так как уничтожение ключа означает, что вся информация, оставшаяся зашифрованной на этом ключе, становится также недоступной.
Гораздо более серьезной проблема смены ключей становится при передаче зашифрованной информации по каналам телекоммуникаций. Для передачи и нормального приема зашифрованного сообщения необходимо, чтобы на обоих концах канала связи был заранее известен один и тот же секретный ключ. В этом случае схема передачи информации выглядит следующим образом
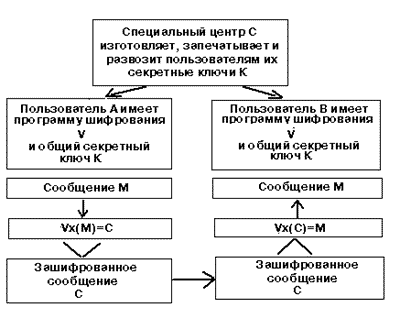
В такой системе, как легко видеть, на центр изготовления и рассылки ключей ложатся функции не только снабжения пользователей ключами, но и ответственность за сохранение их в секрете при изготовлении и доставке. А поскольку в случае утечки информации в результате компрометации ключей в такой системе практически невозможно доказать, где произошла компрометация (у одного из пользователей или в центре С), то обычно принимается, что центр гораздо надежней и важней и потому на него же возлагаются обязанности по контроля за всеми ключами на протяжении всего цикла от изготовления до их уничтожения у пользователя.
Таким образом, вопрос о том, кто является истинным хозяином информации (а значит, и хозяином положения), в такой сети получает однозначный ответ.
В этом случае центр С выступает также и как гарант подлинности передаваемых сообщений, так как, если пользователю В удастся с помощью секретного ключа К, доставленного из центра, расшифровать сообщение М, полученное им от пользователя А, то он уверен, что зашифровать и отправить его мог только обладатель того же ключа К, а это мог быть только А (или другой пользователь, получивший такой же ключ из центра С).
Здесь мы подходим к следующей проблеме. Если в сети обмениваются информацией, скажем, 100 пользователей, то потенциально возможных связей между ними (99х98)/2=4851, т. е. для обеспечения независимого обмена информацией между каждой парой пользователей центр С должен изготовить и разослать 100 комплектов по 99 ключей в каждом, сформированных надлежащим образом из исходного набора 4851 ключей. если ключи сменяются хотя бы 1 раз в месяц, то в течение года необходимо изготовить 58212 исходных ключей, сформировать из них 1200 комплектов по 99 ключей в каждом и развести всем пользователям системы.
И это для сети только из 100 пользователей. А если в сети работают несколько тысяч пользователей, то получится почти как у гоголевского героя "тридцать пять тысяч одних курьеров".
Этот "генетический дефект" традиционных систем обмена шифрованной информацией сразу же был остро почувствован разработчиками коммерческих телекомуникационных сетей при первых попытках использовать шифрование как средство подтверждения подлинности и авторства электронных документов при передаче их по каналам электросвязи 70-х годов.
Даже такие мощные организации в области межкомбанковских расчетов, как S.W.I.F.T. (Международная межбанковская организация по финансовым расчетам), вынуждены идти на риск и прибегать при рассылке части секретных ключей к услугам обычной почты.
Это дает возможность несколько снизить расходы, но необходимость применять дополнительные меры защиты секретных ключей, пересылаемых в конвертах, делает удешевление не столь ощутимым.
Новые принципы современной криптографии
Размышления о том, как избавиться от недостатков традиционных систем криптографической защиты, связанных с необходимостью содержать мощную и дорогую службу изготовления секретных ключей м снабжения ими пользователей, привели двух американских исследователей У. Диффи и М. Хеллмана в 1976 году к следующим принципиально новым идеям.
Предполагая, что пользователи имеют некоторую общеизвестную надежную процедуру (программу) шифрования и общеизвестные же процедуры преобразования исходный ключей, можно изобразить схему формирования парой пользователей А и В общего секретного ключа К для шифрования/расшифрования.
Главным пунктом, принципиально отличающим данную схему получения пользователями общего секретного ключа от традиционной, является то, что обмен открытыми ключами f(x)и f(y) производится по любому доступному каналу связи в открытом виде.
При этом должна быть гарантия, что по перехваченным в канале открытым ключам f(x)и f(y) практически невозможно получить общий ключ К, не зная хотя бы один из исходных секретных ключей x, y. В качестве такой гарантии в данном случае выступает сложность известной математической проблемы, которую приходится решать в ходе вычислений К по f(x)и f(y).
Если в качестве ключей x и y выбираются случайные целые числа из 512 бит каждое, то для вычисления К по f(x)=ax mod p и f(y)=ay mod p с целыми a и p (также по 512 бит каждое) необходимо проделать работу не менее чем из 1024 операций, что потребовало бы более 1000 лет работы любой современной супер-ЭВМ.
Таким образом, вычисление общего секретного ключа К только по открытым ключам f(x)и f(y) является практически невыполнимой задачей, что позволяет применять ключ К для надежного зашифровывания информации.
Другой принцип, предложенный У. Диффи и М. Хеллманом для решения проблемы снабжения пользователей сети ключами шифрования/расшифрования получил название открытое шифрование.
Для зашифрования и расшифрования информации используются различные ключи, которые, хотя и связаны между собой, но устроены так, что вычислить по одному из них (открытому) второй (секретный) практически невозможно (в том же смысле, что и выше).
Первое практическое воплощение принцип открытого шифрования получил в системе RSA, разработанной в 1977 году в Массачусетском Технологическом Институте (США) и получившей свое название от первых букв фамилий авторов: R. Rivest, A. Shamir, L. Adelman.
Идея авторов состояла в том, что взяв целое число n в виде произведения двух больших простых чисел n=p*q, легко подобрать пару чисел e и d, таких, что l
В качестве открытого ключа шифрования в системе RSA выступает пара Y=(n,e), а секретным ключом для расшифрования сообщений является число d.
Процедура шифрования сообщения M, рассматриваемого как целое число, меньшее n (при необходимости длинное сообщение разбивается на отрезки, шифруемые независимо), состоит в вычислении значения
C=Me mod n.
Расшифрование осуществляется аналогично с использованием секретного ключа d:
M=Cd mod n.
Математически строго можно доказать, что определение по паре чисел n, e секретного ключа d, не проще разложения на множители числа n, т. е. нахождения p и q. Задача же разложения на множители целого числа изучается в математике с древнейших времен и известна как очень сложная вычислительная задача. На настоящий момент разложение числа из нескольких сотен десятичных знаков потребует на современных ЭВМ тысячи лет непрерывной работы.
Кроме системы RSA известен целый ряд систем открытого шифрования, основанных на других сложных математических задачах, таких как задача об укладке ранца, задачи декодирования линейных кодов и т. д. Однако все они не получили достаточно широкого распространения и являются в основном теоретическими разработками.
С идейной точки зрения разница между системами открытого распределения ключей и открытого шифрования не столь принципиальна: каждая из них при небольшой модификации может использоваться как для шифрования, так и для распространения секретных ключей по открытым каналам связи.
Переход от открытого шифрования к открытому распределению ключей достаточно прозрачен: отправитель шифрует и передает с помощью системы открытого шифрования секретный ключ, на котором потом будут традиционным способом шифроваться информация. Общий секретный ключ, получаемый при открытом распределении ключей, можно использовать непосредственно для шифрования, побитно складывая его с передаваемым сообщением, в результате чего получается система открытого шифрования. Поэтому для именования обеих систем часто употребляют единый термин "системы с открытым ключом", не уточняя, какой тип обмена сообщений или ключей имеется в виду.
Дополнительным соображением в пользу единого именования систем является то, что с практической точки зрения их эффективнее использовать лишь для распределения секретных ключей, осуществляя шифрование информации традиционным способом. Дело в том, что основной операцией в этих системах является возведение в степень по модулю.
500-1000-битовых чисел, что при программной реализации в несколько десятков раз медленнее, чем шифрование того же размера данных стандартным алгоритмом (например, DES). Поэтому для быстрой обработки большого потока сообщений применяют специализированные процессоры, выполняющие данную операцию, или же используют системы с открытым ключом только для получения секретного ключа шифрования.
Цифровая (электронная) подпись
Принципы открытого распределения ключей и открытого шифрования, решая наиболее трудоемкую проблему изготовления и рассылки секретных ключей для шифрования и предоставляя абонентам открытых систем возможность передать конфиденциальную информацию без непосредственного контакта и предварительного обмена ключами, поставили во главу угла проблему подлинности партнерства и авторства принимаемых сообщений.
Развитие деловой переписки в электронном виде требовало не только возможности самому получателю удостовериться в подлинности документа, но и возможности доказать авторство документа третьей стороне, например, суду.
Классическое распределение ключей посредством центра решало данную проблему частично: автором правильно расшифрованного сообщения мог быть только тот, кто знал ключ, то есть отправитель, получатель и, возможно, центр.
Кроме того, предъявление третьему лицу документа вместе с ключом шифрования означает, что становятся известными и все остальные сообщения, переданные с помощью данного ключа, что не всегда приемлемо, а обеспечить всем по разовому ключу на каждое сообщение не представляется возможным.
Необходим был электронный аналог физической подписи, обладающий двумя основными свойствами:
- воспроизводима только одним лицом, а подлинность ее может быть удостоверена многими;
- неразрывно (посредством листа бумаги) связана с данным документом и только с ним.
Путь создания электронной подписи также был предложен У. Диффи и М. Хеллманом и основывался, как и при открытом шифровании, на использовании пары связанных между собой ключей (секретного и открытого). Их идея состояла в том, чтобы в системе открытого шифрования поменять роли секретного и открытого ключей: ключ подписывания сделать секретным, а ключ проверки - открытым.
Если при этом сохраняется свойство, что по открытому ключу с вычислительной точки зрения нельзя в обозримое время найти секретный ключ подписывания, то в качестве электронной подписи может выступать само сообщение, подписанное на секретном ключе.
Тем самым подписать сообщение может только владелец секретного ключа, но каждый, кто имеет его открытый ключ, может проверить подпись, обработав ее на известном ключе.
В системе открытого шифрования RSA секретный и открытый ключи - числа e и d - равноправны, что позволяет непосредственно применить данную конструкцию и получить цифровую подпись RSA.
Использование в качестве цифровой подписи результата шифрования не является общим методом, а скорее служит иллюстрацией перехода от прежнего способа подтверждения подлинности, основанном на наличии у сторон одинакового секретного ключа, к системам с двумя различными ключами.
В общем случае под цифровой подписью понимается числовое значение, вычисляемое по сообщению с помощью секретного ключа подписывающего. Проверка цифровой подписи осуществляется общеизвестной процедурой на основании открытого ключа.
Открытый и секретный ключи жестко связаны между собой, но с вычислительной точки зрения как невозможно найти по открытому ключу секретный, так и подобрать саму подпись, исходя только из известной процедуры проверки.
Среди подписей, не использующих открытое шифрование, наибольшую известность получила подпись американского ученого Эль-Гамаля (T. ElGamal). В его алгоритме открытый ключ Y, как и открытом распределении ключей У. Диффи и М. Хеллмана, есть Y=ax mod p.
Подпись t состоит из пары чисел R и S, где R=ak mod p вычисляется для случайно взятого значения k, а S=M+xrmodp-1.
Проверка подписи состоит в проверке соотношения aS=YR*RM mod p.
Технология обработки и обмена электронными документами
Цифровая подпись в сочетании с открытым распределением ключей и/или открытым шифрованием позволяет организовать защищенный обмен электронными документами с подтверждением подлинности как абонента так и самих сообщений, не прибегая к услугам дорогостоящей службы изготовления и развоза секретных ключей. При этом электронным документам может быть придана юридическая значимость.
Единственная проблема, которая не может быть решена при заочном общении пользователей, это - обеспечение их достоверным каталогом открытых ключей пользователей (достаточно ограничиться открытыми ключами подписи). Однако, в большинстве открытых систем имеется администратор системы, осуществляющий прием и регистрацию пользователей. Естественно возложить на него и сбор и предоставление открытых ключей.
Регистрация пользователей проводится так:
- Администратор сообщает свой открытый ключ подписи.
- Пользователь А генерирует секретные ключи шифрования и подписи x, u
- и предъявляет для регистрации соответствующие открытые ключи X, U.
- Составляет каталоги открытых ключей подписи A, X.
- Составялет каталоги открытых ключей шифрования A, U,
- подписывает и рассылает пользователям.
- Проверяет подпись Администратора под каталогами, после чего использует их в работе.
Работа с электронными документами строится следующим образом:
|
и подписи x, u и документ М |
и подписи y, w |
|
|
|
|
|
|
|
|
проверка подписи notary(Y, M, t) оформляет квитанцию N sign(y, N)=s |
|
проверка подписи notary(Y, M, t) |
|
При такой организации в отличии от первоначальной схемы администрация системы не имеет доступа к секретным ключам пользователей, а значит - и к защищаемой с помощью их информации. За администрацией осталась лишь возможность подменить в каталоге открытые ключи одного из абонентов (или включить фиктивного абонента), от его имени войти в контакт и получить предназначенное тому сообщение. Однако при возникновении конфликта на этой почве подпись администрации под подложном каталогом будет основанием для привлечения ее к ответственности.
Чья подпись лучше?
Поводом для развернувшейся в прессе полемики послужила публикация Национальным институтом стандартов и технологий США проекта национального стандарта цифровой подписи (1991).
В качестве стандарта было предложено взять алгоритм подписи Эль-Гамаля, модернизированный на основе идей Шнорра, что вызвало негативную реакцию разработчиков, ориентирующихся на систему RSA.
Оценивая надежность этих подписей, надо представлять, что подписи основываются на разных математических задачах:
- подпись RSA - на задаче разложения целого числа на простые множители;
- подпись Эль-Гамаля - на задаче дискретного логарифмирования (по заданным
числам a и b и простому числу p найти целое число
x, 1
p-1 , такое что ax mod p=b).
Обе эти задачи имеют высокую оценку сложности для больших целых чисел p и n, но элементарные операции в них разные: при разложении решается двоичная система линейных уравнений, а при логарифмировании - система уравнений по модулю p-1.
В результате реальная оценка сложности задачи дискретного логарифмирования оказывается примерно на три порядка выше оценки сложности разложения (для числе из 200-500 бит).
Более того, все известные методы дискретного логарифмирования могут быть использованы также и для разложения чисел, но наряду с ними существуют методы, применимые только для разложения.
То есть задача разложения более уязвима для нападения и с точки зрения надежности приоритет должен быть за подписью Эль-Гамаля.
Аналогичная картина наблюдается в вопросе выбора параметров. Для построения каждой из систем требуется выбрать простые числа специального вида и проверить для них множество условий. Очевидно, что при таких затратах для подписи Эль-Гамаля, где используется всего лишь одно простое число на всех, выбор его может быть выполнен более тщательно, чем каждая пара простых в подписи RSA.
По потребительским качествам подпись Эль-Гамаля несомненно лидирует по размеру самой подписи, которая может быть в несколько раз меньше, чем в системе RSA, что весьма существенно для загруженных телекоммуникационных сетей.
Что касается временных характеристик, то подписывание по Эль-Гамалю осуществляется в несколько раз быстрее, чем в RSA. В проверкой подписи дело обстоит наоборот, если в RSA используется открытый ключ полного размера, то проверка подписи Эль-Гамаля осуществляется несколько быстрее, если в RSA применен короткий открытый ключ, как это делается во многих приложениях, то система RSA может превосходить подпись Эль-Гамаля по времени проверки.
Уже из такого беглого сравнения подписей видно, то они основываются на близких математических задачах, имеют высокую надежность и используют сходный алгоритмический аппарат.
В этом смысле ни одна из них не обладает безусловным преимуществом. При выборе подписи для практического применения в открытых системах целесообразно, видимо, делать упор на эксплуатационные характеристики подписей и их соответствие техническим возможностям системы. Вполне разумным может оказаться использование разных подписей: в зависимости от распределения вычислительных мощностей в открытой системе и потока сообщений иногда имеет смысл задействовать одновременно оба вида подписи, чтобы обеспечить равномерную нагрузку сети и повысит ее пропускную способность.
