Графы и сети
Ученые начали интересоваться сетевыми структурами, когда Интернета еще и в помине не было. Зато существовали транспортные и энергетические сети, социальные и экологические системы, сети промышленных предприятий. Для формалистов-ученых было важно, что все они устроены похожим образом и хорошо описываются теорией графов. Граф — это структура, состоящая из вершин (узлов), соединенных связями (дугами). Возьмем, к примеру, сеть аэропортов. Узлами в ней являются аэровокзалы, а дугами — рейсы. Другой пример — сеть автодорог: узлы — города, связи — дороги. Понятно, что количество узлов в этих графах будет постоянно возрастать. Поскольку новые узлы добавляются непредсказуемым образом, то для изучения случайного графа применяется теория вероятностей.
|
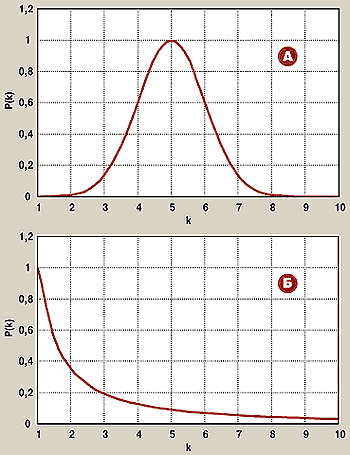
| Рис. 1. Законы распределения: а - экспоненциальный; б - показательный |
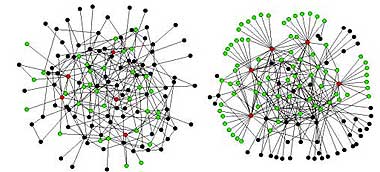
Важной характеристикой, которая может быть получена для случайного графа, служит вероятность того, что узел связан с другими k узлами. Эта величина называется распределением связности. Имеющиеся сети можно разделить на два класса, один из которых характеризуется экспоненциальным распределением связности, а другой — показательным (рис. 1). Основываясь на форме графика, американский физик Альберт Ласло Барабаши (www.nd.edu/~alb) назвал сети с показательным распределением бесступенчатыми (scale-free). Оказалось, что бесступенчатые сети обладают некоторыми полезными свойствами. В экспоненциальных сетях каждый узел связан примерно с одинаковым числом других узлов. В бесступенчатых же сетях количество связей у различных узлов неодинаково: имеются сильно связанные фрагменты сети и менее связанные. Если попытаться изобразить структуру сети при помощи, например, программы Pajek (vlado.fmf.uni-lj.si/pub/networks/pajek/pajekman.htm), то получится приблизительно такая картинка, как на рис. 2. Красным цветом обозначены узлы сети, имеющие наибольшее число связей, зеленым — те, которые связаны с красными, черным — все остальные. Если часть узлов вывести из строя, то работоспособность сети, вообще говоря, может измениться (вспомним хотя бы пресловутый разрыв хозяйственных связей после распада СССР). В такой ситуации бесступенчатые сети демонстрируют более высокую устойчивость, чем экспоненциальные. Если переложить эти рассуждения на язык Интернета, то выведение из строя отдельных узлов сети называется атакой. А значит, в научных исследованиях Барабаши речь идет, ни много ни мало, о безопасности и надежности Сети перед хакерской угрозой.
|
| Рис. 2. Графы экспоненциальной (слева) и бесступенчатой сетей |
Кругосветное путешествие трафика
Для того чтобы результаты, полученные в теории графов и при исследовании реальных сетей, применить к Интернету, нужно собрать данные об огромном количестве компьютеров, подключенных к глобальной Сети. На физическом уровне Интернет можно рассматривать как совокупность компьютеров и маршрутизаторов, соединенных между собой каналами связи. Когда пользователь загружает документ в окно браузера, данные совершают долгое путешествие по множеству узлов. Собрав сведения об этих узлах, можно построить своеобразные карты Интернета. Так и поступили исследователи из Bell Labs (www.cs.bell-labs.com/~ches/map). Анализ таких карт (рис. 3) показывает, что на физическом уровне Интернет — бесступенчатая сеть. А значит, он устойчив к случайным сбоям отдельных узлов. Действительно, по результатам мониторинга, около 0,05% узлов Сети находятся в нерабочем состоянии и этот печальный факт никоим образом не сказывается на ее работоспособности. Тем не менее у Интернета все-таки есть слабое место. Сеть неоднородна: в ней имеются более сильно и менее сильно связанные участки. Так вот, если вывести из строя незначительное число узлов с наибольшим количеством связей, Сеть распадется на несколько отдельных фрагментов. Безусловно, чтобы провести успешную атаку на Сеть, хакерам необходимо знать, какие узлы являются наиболее важными. Но если вспомнить, что первоначальной целью создания Интернета было обеспечение наиболее отказоустойчивой связи между компьютерами в военных условиях, то прогресс в развитии Сети не будет казаться столь ошеломляющим.

|
| Рис. 3. Компьютеры в Интернете и физические связи между ними |
Другую угрозу для работоспособности Интернета представляют вирусы. Их распространение в последние десятилетия изучалось в рамках теории диффузии. Согласно этой теории, вирус сможет быстро размножаться лишь в том случае, если степень его «заразности» превышает некий критический порог, который можно точно определить, основываясь на свойствах среды распространения. Как показали исследования группы ученых из Испании и Италии (complex.upc.es/~romu), для бесступенчатых сетей критический порог равен нулю, т. е. даже очень слабый вирус способен заразить всю систему. Этим объясняется тот факт, что считавшийся искорененным вирус I Love You даже год спустя все еще занимал седьмое место среди наиболее часто встречающихся вирусов.
В сетях гипертекста
Попробуем посмотреть на Интернет глазами пользователя. Он, как правило, сталкивается с массой гипертекстовых документов. Если страницы гипертекста — это узлы, а ссылки — дуги, то полученный огромный граф будет представлять всю WWW. Чем может помочь изучение этого графа, например, тем, кто хочет «застолбить» себе достойное место в Сети?
Для ответа на этот вопрос вооружимся последними достижениями науки. Условно разделим все существующие в природе сайты на две категории: «авторитеты» и «концентраторы». Первые содержат много нужной и интересной информации по некоторой теме, вторые — множество ссылок на другие интересные сайты. Чтобы определить, в какую группу попадает страница гипертекста, необходимо вычислить для нее количество исходящих и входящих ссылок (уводящих к другим ресурсам и ведущих к ней с других сайтов).
Как показали исследования специалистов из IBM, AltaVista и Compaq (www.almaden.ibm.com/cs/k53/clever.html), гипертекст тяготеет к «авторитетам», чем напоминает создавшее его человечество. В ходе проведенного эксперимента использовалась специальная программа, которая обработала более 500 Мбайт гипертекстовых страниц и свыше 1,5 млрд. ссылок. Собранная информация позволяет утверждать: структура Интернета неоднородна, в нем можно выделить так называемое ядро (объемом около 56 Мбайт), состоящее из «концентраторов» и «авторитетов»; все остальные — периферийные — сайты обладают небольшим «весом» в сетевом сообществе. В течение своей жизни сайт либо «набирает вес» и входит в ядро, либо в конце концов умирает в забвении. Правда, как и в обычной жизни, наблюдается замкнутый круг: активнее всего входящими и исходящими ссылками пополняются те сайты, «вес» которых в Сети и так велик. Другими словами, богатый становится еще богаче.
Из результатов исследований логично следует практический вывод: для завоевания успеха в сетях гипертекста необходимо активно обмениваться ссылками с другими сайтами. К еще более ценным выводам пришли разработчики поисковых машин, снабдив результаты поиска количественными показателями «сетевого веса» сайта. К примеру, в каталоге Яndex для Web-страницы указывается значение индекса цитирования, который вычисляется по количеству ссылающихся на нее сайтов. Технология PageRank (опять расчет количества ссылок) используется для ранжирования сайтов поисковой машиной Google. Кроме того, если после неудачных поисков в Сети у вас уже возникло желание обзавестись инструментом, позволяющим определить «уровень» сайта, что называется не сходя с места, то Google способен предоставить и такую возможность (рис. 4).
Ну и, наконец, еще один полезный результат: поскольку сайты, обладающие «весом» в Сети, связаны друг с другом, при поиске нужной информации достаточно найти первую релевантную ссылку. Вытащить за это звено всю цепь «полезных» сайтов уже не сложно. Но чтобы найти эту первую ссылку, необходимо быть квалифицированным поисковым агентом.
Когда физики не шутят...
Так как Ласло Барабаши и его коллеги из лаборатории по исследованию сетей Университета Нотр-Дама (www.nd.edu/~networks) — физики, неудивительно, что они посмотрели на WWW и с точки зрения физических достижений (похоже, они взглянули на него со всех возможных точек зрения). Под таким углом пространство гипертекста оказалось похожим (кто бы мог подумать!) на модель конденсата Бозе — Эйнштейна. Долгое время вышеозначенный конденсат существовал лишь в сознании физиков-теоретиков. Но в 1995 г. он был экспериментально получен двумя независимыми группами ученых, кстати говоря награжденными за это достижение Нобелевской премией. В состоянии вещества, которое описывает модель Бозе — Эйнштейна, на одном и том же уровне энергии может находиться неограниченное число частиц. Как же соотнести эту физическую модель со страницами гипертекста? Каждая страница Сети представляется как отдельный энергетический уровень конденсата Бозе — Эйнштейна, а каждая ссылка на нее (т.е. входящая ссылка) — как частица, находящаяся на данном уровне. Таким образом, новый узел в Сети, который содержит ссылки на некоторые страницы, но еще не имеет входящих ссылок, будет представлен как незанятый энергетический уровень, а самый густонаселенный уровень будет соответствовать наиболее весомому «авторитету» в Сети.
Модель Бозе — Эйнштейна является одной из наиболее подробно изученных задач в атомной физике. В частности, расчеты показывают, что в зависимости от формы распределения частиц по уровням возможны два сценария развития событий. Один из них хоть и подтверждает принцип «богатый станет еще богаче», все же не приводит к «чистой победе» — образуется несколько густозаселенных уровней. Другой сценарий как раз и описывает конденсацию — почти все частицы оказываются на одном, самом заселенном уровне. На языке пользователей Интернета это означает, что все сайты в Сети начнут ссылаться на один узел — своего рода непререкаемый авторитет. Для того чтобы определить, какой же из этих двух сценариев будет реализован в действительности, пока не хватает экспериментальных данных. Время покажет.