В настоящее время можно найти немало коммерческих шахматных программ, играющих в силу международного мастера, среди которых особенно отличились Fritz, Junior, Shredder, объединенные эпитетом Deep. Они добились серьезных успехов в соревнованиях с гроссмейстерами. Постоянный интерес читателей нашего журнала к программированию древней игры заставил нас обратиться к Вадиму Чижову, одному из лауреатов конкурса Microsoft Office Extensions за второе полугодие 2002 г. (www.microsoft.ru/offext), с просьбой рассказать о его разработке — «Шахматы 64» и о принципах, положенных в основу. (От редакции.)
В «Шахматах 64» использованы методы, типичные для большинства шахматных программ. Так, в основе ее алгоритма лежит минимаксный анализ, позволяющий выбирать ход, наилучший для данной позиции. Выполняется он с помощью поиска по дереву позиций. В его корне ищется лучшая последующая позиция за того игрока, которому предстоит сделать ход. На следующем уровне дерева позиций идет поиск лучшего хода за противника и т. д. При этом результаты поиска по дереву связываются с чередованием позиций, имеющих максимальные и минимальные оценки, поэтому такой метод нередко называют минимаксингом. В качестве оценочной используется функция, учитывающая условную «стоимость» шахматных фигур, защищенность королей, степень контроля за центром доски, подвижность фигур, наличие объектов для атаки, структуру пешечного построения и многое другое. Рассмотрим пример минимаксного анализа позиции, приведенный на рис. 1.
|
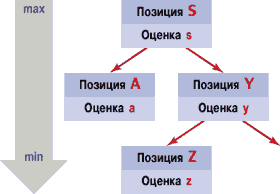
| Рис. 1. Неглубокое отсечение |
Пусть в позиции S ход принадлежит нам. При этом в нашем распоряжении есть несколько возможных ходов, два из которых показаны на рис. 1. В результате одного из ходов возникает позиция А, полностью проанализированная (ее количественная оценка — а), а в результате другого — позиция Y с оценкой y. Пусть, далее, следующий ход из этой позиции приводит к новой позиции — Z, проанализированной с оценкой z. Покажем, что если z<a, то результат позиций, следующих за Y, не изменит оценки S. Допустим, величины s и y — это значения оценок в узлах S и Y соответственно. Очевидно, что y<z, так как в позиции Y ход остается за противником, который выберет ход, приводящий к позиции с наименьшей оценкой. Также можно убедиться, что s>a. Следовательно, получим, что y<z<a<s, и стало быть, неизвестное значение оценки y в позиции Y не изменит величину s. После анализа позиции Z остальные ветви дерева, выходящие из Y, могут быть отброшены. Обобщение данного случая лежит в основе алгоритма альфа-бета отсечения, более эффективного, чем обычный минимаксный алгоритм.
Многие игры, в том числе и шахматы, допускают перестановку ходов, что приводит к необходимости анализа повторяющихся позиций. Так, если все ходы допускают перестановку, то при необходимости анализа повторяющихся позиций та, что на глубине 2k полуходов, может быть достигнута (k!)2 способами. Чтобы повторно не анализировать позиции, обычно используют таблицу перестановок.
Позиции, для которых велика вероятность значительного отклонения величины значения оценочной функции от истинного значения, принято называть неустойчивыми, и их анализ следует проводить до достижения относительно спокойных позиций. К неустойчивым в шахматах принято относить некоторые позиции, возникающие после взятия или объявления шаха.
Алгоритм выбора хода в «Шахматах 64», или «движок» программы, реализован с помощью средств Visual Cи++ 6.0 в виде динамически подключаемой библиотеки (DLL), а интерфейс — в виде документа Microsoft Word.
На рис. 2 приведено отображение на экране позиции и заставки программы.
Вот пример игры программы «Шахматы 64» против Josh—Age 12 с рейтингом 2100 из Chessmaster 8000 (регламент — 3 мин на партию на ПК, оснащенном процессором Pentium III с тактовой частотой 366 МГц). Текст партии оформляется в английской нотации.
[Date «7-12-2003»] [White «Josh—Age 12»] [Black «Шахматы 64»] [Result «0-1»]
1.e4 e5 2. Bc4 Nc6 3. Nf3 Nf6 4. d3 d5 5. exd5 Nxd5 6. Bd2 f6 7. Bxd5 Qxd5 8. Nc3 Qd8 9. h3 Bf5 10. Nh4 Be6 11. f4 exf4 12. Nf3 Bd6 13. Nb5 O-O 14. Qe2 Re8 15. O-O-O Bxa2 16. Qf2 Be5 17. b3 Qd5 18. Nxe5 Nxe5 19. Nc3 Qxb3 20. Qc5 f3 21. gxf3 Qb6 22. Qxb6 axb6 23. Nb5 Re7 24. Rhe1 Be6 25. Bc3 c6 26. f4 Ng6 27. Rxe6 Rxe6 28. Nc7 Ree8 29. f5 Nf4 30. Nxa8 Ne2+ 31. Kd2 Nxc3 32. Kxc3 Rxa8 33. Kd2 b5 34. Ke3 Re6+ 35. Kf3 Re5 36. Kf4 Re2 37. Kf3 Rxc2 38. Ra1 Rh2 39. Ra8+ Kf7 40. Rb8 Rxh3+ 41. Ke4 Rh4+ 42. Ke3 g5 43. Rxb7+ Ke8 44. Rc7 Rf4 45. Rxc6 Rxf5 46. d4 h5 47. Ke4 Rf4+ 48. Ke3 Rf1 49. Ke2 Rf5 50. Re6+ Kf7 51. Rc6 h4 52. Rc7+ Kg6 53. Rc1 Rd5 54. Ke3 h3 55. Rc8 Kc5 56. Rc2 g4 57. Rh2 Ke6 58. Rh1 b4 59. Rh2 b3 60. Kd3 Rb5 61. Re2+ Kf7 62. Rb2 g3 63. Kc4 h2 64. Kxb5 h1=Q 65. Kb4 g2 66. Rxg2 Qxg2 67. Kxb3 Qd2 68. Kc4 Ke6 69. Kc5 f5 70. Kc4 f4 71. Kd5 f3 72. Kb6 f2 73. d5+ Qxd5 74. Kc7 f1=Q 75. Kb6 Qd6+ 76. Ka5 Qfa6# 0-1 (Белые проиграли.)
В Интернете можно найти много материалов по шахматным программам, но практически отсутствуют «фирменные» секреты коммерческих продуктов. Рекомендую поисковую систему Google, так как она позволяет более эффективно находить научные публикации.
Вадим Чижов, chizhov_vadim@mail.ru