ИТ представляют собой одну из тех немногих областей, которые характеризуются наличием значительных резервов гибкости, обеспечивающей проекту увеличение стоимости. Оценить гибкость можно с помощью методики "анализа реальных опционов".

ИТ присуща значительная гибкость, которая в реальном проекте, несомненно, способна увеличить его стоимость, в сочетании с возможностью активного вмешательства в ход проекта со стороны менеджмента компании.
Реальные опционы: подход к оценке гибкости бизнеса
Структура инвестиционного параметра NPV [1], с помощью которого обычно экономически обосновывается инвестиционный проект, предполагает единственный сценарий его будущего развития. Она не позволяет ни оценить вероятность изменений в самом проекте, компании и рыночной среде, ни выразить результаты активного вмешательства его руководства в соответствии с вновь открывающимися возможностями в финансовых терминах.
Максимально приблизить полученные оценки к истинному значению можно с помощью методики «анализа реальных опционов» (Real Options Analysis, ROA) [2], позволяющей адекватно учитывать особенности проекта. При этом стоимость проекта может быть более точно описана модифицированным (иначе называемым RO-стратегическим) NPV:
RO-стратегический NPV =
= классический NPV + стоимость реального опциона (2)
Для того чтобы достоверно отразить, насколько увеличится стоимость предприятия после внедрения программного комплекса, необходимо оценить опционы, связанные с возможностью будущих изменений в ходе реализации проекта. В отношении высоких технологий здесь скрыт немалый потенциал. ИТ представляют собой одну из тех немногих областей, которые характеризуются наличием значительных резервов гибкости, обеспечивающей проекту увеличение стоимости.
Что собой представляют реальные опционы и каковы их истоки?
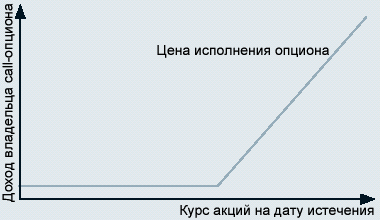
Понятие «опцион» пришло в «реальную» сферу из финансовой области, где сегодня он наиболее распространен как один из основополагающих структурных компонентов многих финансовых инструментов. В финансах опцион (точнее, его европейская разновидность) представляет собой право (но не обязательство) в определенный момент приобрести или продать актив по оговоренной заранее цене. Так, опцион на покупку (call-опцион) позволяет застраховать (хеджировать) риски, связанные с увеличением цены интересующего актива. В то же время он не обязывает потенциального покупателя совершать сделку, если по каким-то причинам делать это для него невыгодно. Опцион на продажу (put-опцион) обеспечивает возможность более выгодного сбыта финансового инструмента в условиях падения его цены. Естественно, подобное право не может быть бесплатным. Возможности, которые он предоставляет инвестору, имеют определенное финансовое выражение.
Вполне естественно, что определенной стоимостью будет обладать и право принимать решения, связанные с нефинансовыми активами. Термин «реальные опционы» впервые ввел Стюарт Майерс в 1977 году применительно к опционной оценке нефинансовых активов, в частности, для рассмотрения вопросов инвестирования в сферу многогоэтапных исследований и разработок.
ROA применяется в таких крупных корпорациях, как Airbus, General Electric, Hewlett-Packard, Intel, Toshiba и др. Однако есть немало компаний (почти половина из них), которые однажды попытавшись внедрить эту методологию в свою практику, отказываются (в основном из-за сложности) от ее дальнейшего применения.
Стоимость гибкости реального проекта напрямую зависит от неопределенности в бизнесе, связанной как с его масштабом, так и с будущей прибыльностью. Сама по себе гибкость не обладает стоимостью. Она ценна только в сочетании с неопределенностью условий его развития, в которых она может быть практически использована. При полностью определенном будущем гибкость системы, позволяющая что-то менять в бизнесе, не имеет никакой ценности. Наиболее наглядные примеры реальных опционов обычно связаны с нефтегазовой отраслью, в которой реальным опционом может быть, в частности, покупка компанией права на добычу нефти из определенных скважин в течение какого-то времени. При этом неопеределенность появляется как в неточности геологораведочных оценок нефтяных запасов, так и в связи с возможным изменением цен на нефть. Истинная стоимость такого права, в данном случае права на добычу нефти из определенных скважин в течение какого-то времени, зависит от нескольких факторов (и может значительно отличаться от объявленной государством). Правильная его оценка позволит принять обоснованное решение: вкладывать деньги компании в немедленную разработку скважины, отказаться от этих инвестиций или приобрести право на отложенное решение, когда внутренние и рыночные условия будут более определенными.
Для других областей прозрачное представление реальных опционов может быть не столь характерным. Одной из наиболее перспективных областей применения методологии ROA являются ИТ. Здесь право осуществлять определенные действия выражено не так явно. Различные программные и аппаратные платформы, которые используются в коммерческих организациях, обладают возможностями, позволяющими при необходимости изменять структуру и масштаб бизнеса. Эти возможности не востребованы в текущих и прогнозируемых условиях, а следовательно, не учитываются в традиционном NPV. Тем не менее они могли бы получить применение и принести существенную прибыль проекту впоследствии при разрешении неопределенности. Способность ИТ к масштабированию при хорошей рыночной конъюнктуре позволит бизнесу активно расширяться. В случае ухудшения рыночных условий потери проекта ограничиваются ранее сделанными в продукт инвестициями. Финансовые потоки, генерируемые таким проектом, напоминают структуру выплат по финансовым инструментам, которые хеджированы соответствующим call-опционом.
Первым и основным этапом расчета ROA является анализ инвестиционного проекта в опционном ракурсе. Его цель — не изучение наиболее вероятного или усредненного сценария, а выявление бифуркационных точек, которые предполагают наличие двух вариантов его развития. Заметим, что вершиной профессионализма в инвестиционном анализе является не только обнаружение, но и осознанное создание таких точек. Следующий этап — расчет стоимости реального опциона.
Подходы к оценке реальных опционов
При переносе методики из финансовой области в реальную аналитик неминуемо сталкивается со значительными трудностями. Даже на финансовых рынках применение многих моделей дает лишь ориентировочные значения стоимости опционов, поскольку они разрабатывались, исходя из идеализированных предположений о финансовом рынке. Что же тогда говорить о реальных активах, свойства которых могут быть существенно иными? К тому же для последних отсутствуют прозрачные и понятные механизмы определения стоимости. Основные различия между финансовыми и реальными опционами, которые следует принимать во внимание при адаптации подхода к их вычислению таковы: реальные активы не являются торгуемыми инструментами с непрерывным ценообразованием, отсутствуют фиксированные хронологические сведения об их стоимости, исполнение опциона существенно растянуто во времени.
Тем не менее на практике уже имеются способы решения таких задач. При выборе подхода аналитик основывается на особенностях природы рассматриваемого проекта, характеристиках рыночной среды, соображениях точности полученного результата, он также учитывает собственный уровнь владения соответствующим методом.
Наибольшим математическим изяществом отличается так называемый классический способ, в рамках которого для вычисления реальных опционов предполагается применение знаменитой на финансовых рынках формулы Блэка-Шоулса. Она в явном виде связывает стоимость опциона с текущей стоимостью актива и его волатильностью, стоимостью исполнения опциона, а также временем до его исполнения.
Для вычисления финансовых опционов необходимо подставить в нее имеющиеся характеристики финансового актива и рынка. В результате можно рассчитать величину соответствующего опциона, рассматривая дополнительно различные сценарии поведения актива в будущем. Получив хорошие результаты применения этой методики на финансовых рынках, аналитики, работающие в «реальной» сфере, закономерно поставили вопрос об использовании этой формулы для расчета стоимости гибкости инвестиционных проектов.
Однако апологеты этого подхода сталкиваются со значительными трудностями обоснования его применимости. Формула Блэка-Шоулса (за ее вывод авторы несколько лет назад были награждены Нобелевской премией) получена в предположении безарбитражного финансового рынка, на котором осуществляется непрерывная и ликвидная торговля финансовыми инструментами.
Прямой перенос этой методики на реальные активы может вызвать оправданные сомнения. Однако аналитики доказали правомерность использования формулы Блэка-Шоулса для ряда инвестиционных проектов в случае, если можно сконструировать такой портфель из торгуемых финансовых инструментов, картина денежных потоков по которым в точности повторяла бы аналогичные платежи по реальным активам (replicating-portfolio assumption).
При этом механизме расчета опциона выглядит довольно просто. Определяется «реплицированный» портфель торгуемых инструментов, устанавливаются его стоимость и волатильность, которые в конечном итоге подставляются в формулу Блэка-Шоулса.
Однако на практике все значительно сложнее. Прежде всего, трудность в обосновании применимости формулы Блэка-Шоулса к вычислению значения конкретного опциона состоит именно в проблеме идентификации «реплицированного» портфеля. Круг проектов, в которых можно это сделать просто, довольно узок. Наибольшую применимость такой подход имеет именно в нефтегазовой области. В других случаях можно установить лишь приближенное соответствие между денежными потоками по реальным и финансовым активам, грубо оценив нижнюю границу стоимости опциона. А зная, по крайней мере, ее минимальное значение, можно доказать состоятельность инвестиционного проекта, традиционное NPV которого отрицательно или равно нулю.
Имеются различные модификации этого подхода. Так, аналитик может не затруднять себя построением «реплицированного» портфеля торгуемых финансовых активов, а ограничиться доказательством его существования, то есть в явном виде сведения об этом портфеле не используются. В формуле же Блэка-Шоулса следует применить «субъективные» данные, например, полученные в результате DCF (discounted cash flow) анализа проекта. В отличие от рыночных сведений о стоимости актива, DCF-анализ строится на предположениях о возможных будущих денежных потоках по проекту, а следовательно, он не в состоянии предоставить объективные данные. В итоге это сказывается на адекватности полученной оценки опциона. Более того, применяя указанную формулу, авторы порой не утруждают себя доказательством существования «реплицированного» портфеля, ограничиваясь ссылкой на «качественный» характер полученных результатов.
Кроме методик расчета реальных опционов, основанных на применении формулы Блэка-Шоулса, есть и другие подходы. Так, один из них предлагает рассматривать NPV проекта (без учета его гибкости) как равновесную стоимость, которой бы обладал соответствующий актив, если бы он торговался на совершенном рынке. При этом значение чистой приведенной стоимости рассчитывается традиционным DCF-способом. Далее в рамках этой модели тщательно исследуются эффекты неопределенности, связанные с гибкостью проекта. В результате на выходе получается биномиальное дерево, в каждой точке ветвления которого стоимость актива с некоторой вероятностью может принимать определенные значения. А отсюда, в частности в рамках риск-нейтрального подхода — один шаг к определению стоимости опционов, которые представляют собой право принимать соответствующие управленческие решения, приводящие систему в одно из двух возможных состояний.
Другие методики, довольно подробно описанные в зарубежной прессе, хотя и имеют одно назначение, существенно различаются по степени обоснованности, а также объективности используемых данных.
Несмотря на сложность выполнения рассматриваемого этапа ROA, в его защиту все же можно привести два довода. Во-первых, разработка соответствующей математической модели, обоснование ее применения к конкретному проекту и ее реализация помогает лучше осознать механизмы опционного ценообразования. Вместе с тем позволяет понять, что определенные права имеют определенную стоимость не из-за того, что столько запрашивает, например, государственная структура или разработчик программного обеспечения, а потому, что это рыночный эффект. Во-вторых, несмотря на субъективные допущения и зачастую сомнительную обоснованность применения, такие подходы дают возможность указать хотя бы минимальное значение стоимости реального опциона, что в итоге может сыграть решающую роль в принятии инвестиционных решений.
Оценка гибкости в сфере ИТ
Информационные технологии — это область с большим «запасом» гибких возможностей. Даже примитивное программное приложение обычно предполагает значительное количество гибких настроек, позволяющих использовать систему в различных конфигурациях. Что же тогда говорить о программных комплексах, которые создаются, исходя из принципа максимальной общности, а к конкретным технологиям работы приспосабливаются путем многоуровневой параметризации? Такими системами, в частности, являются различные программные платформы: операционные системы, СУБД, системы документооборота, а также разнообразные системы ERP-класса, которые обеспечивают применение настраиваемых пакетов прикладных приложений. Информационно-аналитические системы, построенные по технологиям хранилищ данных, которые обладают большими гибкими возможностями по созданию на их основе различных прикладных приложений для анализа хранящихся данных — удобный объект для применения ROA. Реальная стоимость проекта их внедрения может оказаться выше прогнозируемой традиционным подходом за счет реализации в будущем новых приложений, которые поддерживаются рассматриваемой платформой (в частности, приложения для анализа клиентской базы, пассивов и активов, маркетинга банковских услуг и т. п.).
С этой точки зрения может быть интересна работа коллектива под руководством Альфреда Таудеса, выполненная в 1999 году на грант Австрийского научного фонда рамках исследовательского проекта «Адаптивные информационные системы и моделирование в экономике и менеджменте». В качестве объекта исследования они выбрали производственную компанию среднего масштаба, работающую в автомобильной отрасли. Для автоматизации бизнес-процессов в ней использовалась одна из наиболее распространенных в мире ERP-систем. Сложившиеся условия поставили руководство компании перед дилеммой: обновить эту систему или внедрить продукт нового поколения того же разработчика. Апологетами первого варианта стала часть акционеров компании, утверждавшая, что пользователей вполне удовлетворяют текущая функциональность и производительность системы, в то время как существуют значительные технологические и организационные риски, связанные с переходом на новую систему. Тем более что стоимость последнего проекта, рассчитанная по традиционной формуле NPV, оказалась отрицательной, и это позволяло без угрызений совести отвергнуть его. За внедрение новой системы выступили ИТ-менеджеры предприятия, объясняя свою позицию преимуществами, связанными с использованием технологически более совершенной платформы, что помогло бы компании стать более конкурентоспособной, динамичной и прибыльной. Однако качественного описания пользы от новой системы оказалось недостаточно, пришлось провести анализ реальных опционов, связанных с открывающимися для компании возможностями, которые могут появиться в связи с переходом на систему нового поколения. Такие возможности были очевидны, в частности, удобное предоставление менеджерам по продажам информации о клиентах и сделках, внедрение документооборота для обеспечения инженерной деятельности, поддержка технологий электронной коммерции и др.
Они применили классический подход к оценке реальных опционов. Прежде всего, в проекте были определены источники прибыли и все статьи инвестиционных затрат (в построенной модели прибыль получалась за счет экономии ресурсов при эксплуатации системы). Следующим шагом стало рассмотрение возможности применения формулы Блэка-Шоулса для оценки реального опциона. Оказалось, что для данного случая возможно построить «реплицированный» портфель, составленный из публично торгуемых финансовых активов, используя с этой целью ценные бумаги самой компании и фирмы-разработчика ПО. В частности, было учтено, что экономия, которую приносила система, была прямо пропорциональна количеству транзакций, которые, в свою очередь, коррелировали с объемом продаж компании, а следовательно, со стоимостью ее акций. В результате реализации модели и расчета по формуле Блэка-Шоулса было выведено минимальное значение стоимости опциона, которое оказалось достаточно большим, чтобы получить расширенное NPV в область положительных значений. В итоге, руководство компании приняло решение о внедрении системы нового поколения.
ROA, как показывает западная практика, может служить мощным аналитическим инструментом, дополняющим возможности традиционных DCF-техник. Тем не менее в условиях, когда даже в ИТ-сфере DCF является чем-то диковинным, рано говорить о широком применении второго этапа ROA, предполагающего использование строгих математических моделей. Но все же хочется верить, что в будущем (пусть и не ближайшем) они тоже завоюют свое место под солнцем.
Литература
- Ольга Кляшторная. Оценка ИТ-проектов. Что выбрать? ДИС № 6, 2003.
- Владимир Кузовлев, Владимир Угрына. Искусство быть понятым. ДИС № 2. 2004.
- Боди З., Мертон Р. Финансы.
- Yonghua Ji и др., Real Options And Software Upgrades: An Economic Analysis / XXIII International Conference on Information Systems, 2002.
Владимир Кузовлев — коммерческий директор департамента банковского ПО RS-BankV.6 компании R-Style Softlab, Kuzovlev@softlab.ru
Владимир Угрына — менеджер по маркетингу компании R-Style Softlab, Ugryna@softlab.ru
|
| Рисунок. Доходная диаграмма для call-опциона |