Невозможно освоить высшую математику по-настоящему, не овладев навыками доказательства теорем. Решающую роль здесь играет самостоятельная работа. Программный продукт «ТеорМат» — средство для активного и глубокого изучения теоретических основ математического анализа. «ТеорМат» создает среду для доказательства теорем и позволяет следить за их корректностью.
Во время доказательства теоремы на экране появляется поле доказательства, содержащее полную информацию о том, что дано (или уже доказано) на данный момент и что требуется доказать.
Докажем, например, теорему о пределе суммы двух последовательностей. Она гласит: «Если последовательности {an}, {bn} имеют конечные пределы A и B, то предел последовательности {an + bn} существует и равен A+B». В начале процесса поле доказательства имеет вид
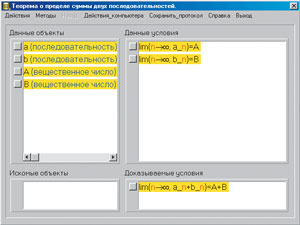
Желтым фоном выделены новые условия и объекты, т. е. те, которых не было на предыдущем шаге доказательства, красным цветом — переменные, локальные для данного условия.
Поле доказательства не только служит для визуализации состояния доказательства, но и является рабочим столом, где действует пользователь. Если он отметит некоторое условие, содержащееся в поле доказательства, то программа предложит список возможных преобразований этого условия. Далее пользователь выбирает нужное преобразование из предложенного списка, а программа его выполняет.
Так, пусть поле доказательства содержит условие lim(n→∞, a_n)=A (предел последовательности {an} равен A). Если пользователь отметит это условие, то в списке возможных преобразований будет содержаться преобразование «Применить определение предела последовательности». В случае выбора данного преобразования отмеченное условие будет заменено условием ∀ε>0 ∃N: ∀n≥N ![]() |a_n - A| < ε (для любого ε>0 существует такое натуральное число N, что для любого натурального n≥N выполнено неравенство |a_n - A| < ε). Применим это преобразование ко всем условиям поля доказательства, изображенного на предыдущем рисунке. Поле доказательства примет вид
|a_n - A| < ε (для любого ε>0 существует такое натуральное число N, что для любого натурального n≥N выполнено неравенство |a_n - A| < ε). Применим это преобразование ко всем условиям поля доказательства, изображенного на предыдущем рисунке. Поле доказательства примет вид
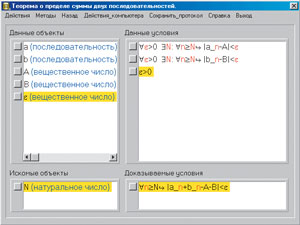
В разделе «Доказываемые условия» вместо ожидаемого условия ∀ε>0 ∃N: ∀n≥N ![]() |a_n + b_n - A - B|< ε мы видим ∀n≥N
|a_n + b_n - A - B|< ε мы видим ∀n≥N ![]() |a_n + b_n - A - B|< ε. Это объясняется тем, что программа «ТеорМат» выполняет некоторые действия автоматически, облегчая работу пользователя. Информацию об автоматических действиях, проделанных компьютером на данном шаге, можно получить, нажав пункт меню «Действия_компьютера». В нашем примере, согласно общим принципам доказательства, при доказательстве условия ∀ε>0 ∃N: ∀n≥N
|a_n + b_n - A - B|< ε. Это объясняется тем, что программа «ТеорМат» выполняет некоторые действия автоматически, облегчая работу пользователя. Информацию об автоматических действиях, проделанных компьютером на данном шаге, можно получить, нажав пункт меню «Действия_компьютера». В нашем примере, согласно общим принципам доказательства, при доказательстве условия ∀ε>0 ∃N: ∀n≥N ![]() |a_n + b_n - A - B|< ε следует считать: дано число ε>0, число N является искомым объектом и требуется доказать условие ∀n≥N
|a_n + b_n - A - B|< ε следует считать: дано число ε>0, число N является искомым объектом и требуется доказать условие ∀n≥N ![]() |a_n + b_n - A - B|< ε.
|a_n + b_n - A - B|< ε.
Теперь поочередно отметим два первых данных условия и подставим вместо переменной ε выражение ε/2. Затем удалим эти два условия, так как они больше не потребуются. Поле доказательства будет иметь вид.
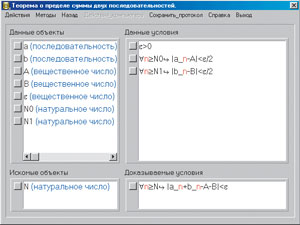
Наряду с преобразованием условий, содержащихся в поле доказательства, пользователь может применять стандартные действия и методы. Меню стандартных действий и методов расположено в левом верхнем углу поля доказательства и состоит из следующих пунктов:
- определить объект;
- применить утверждение;
- рассмотреть случаи;
- доказать вспомогательное условие;
- применить метод доказательства от противного;
- применить метод математической индукции.
Продолжая доказательство рассматриваемой теоремы, определим искомую переменную N = max{N0, N1}. Поле доказательства примет вид
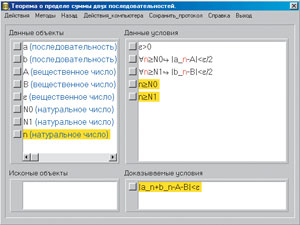
Поочередно подставим переменную n во второе и в третье условия раздела «Данные условия». Тогда будут доказаны неравенства |a_n - A|<ε/2, |b_n - B|<ε/2, из которых компьютер сможет получить доказываемое условие. Компьютер сообщит об успешном завершении доказательства теоремы. Действия пользователя, совершаемые в ходе доказательства, записываются в файл протокола. По этому файлу программа может воспроизводить доказательство в демонстрационном режиме.
Важно, что «ТеорМат» не предусматривает жесткого сценария доказательства и что любое корректное доказательство приемлемо. Поэтому изучение математического анализа с помощью «ТеорМат» носит творческий характер. Программа также снабжена интерактивным учебником, представляющим собой классический курс математического анализа в виде текста с гиперссылками и возможностью самостоятельного доказательства теорем.
Учебный материал, а также база преобразований, совершаемых программой при доказательстве теорем, изменяемы и расширяемы. Эта возможность позволяет опытным пользователям строить собственные теории и проводить собственные исследования. Сейчас в программу «ТеорМат» включены все теоремы, изучаемые в разделе «Предел и непрерывность» университетского курса математического анализа, а также большое количество теоретических задач на подобные темы.
Программа «ТеорМат» может быть использована студентами для самостоятельной тренировки и приобретения навыков доказательства теорем, а также преподавателями при подготовке учебного курса и проведении зачетов и коллоквиумов.
Продукт «ТеорМат» разработан Григорием Ивановым и Романом Константиновым, преподавателями кафедры высшей математики Московского физико-технического института. Версию 3.0 программы «ТеорМат» можно получить бесплатно по адресу http://math.fizteh.ru/teormat. Кафедра высшей математики МФТИ проводит конкурс среди пользователей этой программы.
