Парадоксальный мир невозможных объектов

Наши глаза познавать не умеют
природу предметов.
А потому не навязывай им
заблуждений рассудка.

Расхожее выражение «обман зрения» по сути своей неверно. Глаза не могут обмануть нас, поскольку являются только промежуточным звеном между объектом и мозгом человека. Обман зрения обычно возникает не из-за того, что мы видим, а из-за того, что бессознательно рассуждаем и невольно заблуждаемся: «посредством глаза, а не глазом смотреть на мир умеет разум».

Одним из наиболее эффектных направлений художественного течения оптического искусства (op-art) является имп-арт (imp-art, impossible art), основанный на изображении невозможных фигур. Невозможные объекты представляют собой рисунки на плоскости (любая плоскость двухмерна), изображающие трехмерные структуры, существование которых в реальном трехмерном мире невозможно. Классической и одной из самых простых фигур является невозможный треугольник.

В невозможном треугольнике каждый угол сам по себе является возможным, но парадокс возникает, когда мы рассматриваем его целиком. Стороны треугольника направлены одновременно и к зрителю, и от него, поэтому отдельные его части не могут образовать реальный трехмерный объект.

Невозможный треугольник Пенроуза	Треугольник, воспринимаемый как «возможный»

Собственно говоря, наш мозг интерпретирует рисунок на плоскости как трехмерную модель. Сознание задает «глубину», на которой находится каждая точка изображения. Наши представления о реальном мире сталкиваются с противоречием, с некоей непоследовательностью, и приходится делать некоторые допущения:

Треугольник Рейтерсвэрда

• прямые двухмерные линии интерпретируются как прямые трехмерные линии;
• двухмерные параллельные линии интерпретируются как трехмерные параллельные линии;
• острые и тупые углы интерпретируются как прямые углы в перспективе;
• внешние линии рассматриваются как граница формы. Эта внешняя граница чрезвычайно важна для построения полного изображения.

Человеческое сознание сначала создает общее изображение предмета, а затем рассматривает отдельные части. Каждый угол совместим с пространственной перспективой, но, воссоединившись, они образуют пространственный парадокс. Если закрыть любой из углов треугольника, то невозможность пропадает.

История невозможных фигур

Ошибки пространственного построения встречались у художников и тысячу лет тому назад. Но первым построившим и проанализировавшим невозможные объекты по праву считается шведский художник Оскар Рейтерсвэрд (Oscar Reutersvard), нарисовавший в 1934 г. первый невозможный треугольник, состоявший из девяти кубиков.

Водопад Эшера	«Москва», графика (тушь, карандаш), 50х70 см, 2003 г.

Независимо от Рейтерсвэрда английский математик и физик Роджер Пенроуз повторно открывает невозможный треугольник и публикует его изображение в британском журнале по психологии в 1958 г. В иллюзии использована «ложная перспектива». Иногда такую перспективу называют китайской, так как подобный способ рисования, когда глубина рисунка «двусмысленна», часто встречался в работах китайских художников.

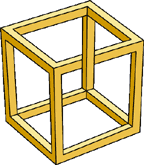
Невозможный куб

В 1961 г. голландец М. Эшер (Maurits C. Escher), вдохновленный невозможным треугольником Пенроуза, создает известную литографию «Водопад». Вода на картине течет бесконечно, после водяного колеса она проходит дальше и попадает обратно в исходную точку. По сути это изображение вечного двигателя, но любая попытка в реальности построить данную конструкцию обречена на неудачу.

С тех пор невозможный треугольник не раз использовался в работах других мастеров. Помимо уже упомянутых можно назвать бельгийца Жоса де Мея (Jos de Mey), швейцарца Сандро дель Пре (Sandro del Prete) и венгра Иштвана Ороса (Istvan Orosz).

Как из отдельных пикселов на экране формируются изображения, так и из основных геометрических фигур можно создавать объекты невозможной реальности. Например, рисунок «Москва», на котором изображена не совсем обычная схема московского метрополитена. Сначала мы воспринимаем изображение целиком, но прослеживая взглядом отдельные линии, убеждаемся в невозможности их существования.

«Три улитки (RDL-куб)», графика (тушь, карандаш), 50х70 см, 2003 г.

На рисунке «Три улитки» маленький и большой кубы ориентированы не в нормальной изометрической проекции. Меньший по размерам куб сопрягается с большим по передним и задним сторонам, а значит, следуя трехмерной логике, он имеет такие же размеры некоторых сторон, что и большой. Сначала рисунок кажется реальным представлением твердого тела, но по мере анализа выявляются логические противоречия этого объекта.

Рисунок «Три улитки» продолжает традиции второй знаменитой невозможной фигуры — невозможного куба (ящика).

«IQ», графика (тушь, карандаш), 50х70 см, 2001 г.	«Вверх и вниз», М. Эшер

Сочетание различных объектов можно найти и в не совсем серьезном рисунке «IQ» (intelligence quotient — коэффициент интеллекта). Интересно, что некоторые люди не воспринимают невозможные объекты из-за того, что их сознание не способно отождествлять плоские картины с трехмерными объектами.

Дональд Е. Симанек высказал мнение, что понимание визуальных парадоксов является одним из признаков того вида творческого потенциала, которым обладают лучшие математики, ученые и художники. Многие работы с парадоксальными объектами можно отнести к «интеллектуальным математическим играм». Современная наука говорит о 7-мерной или 26-мерной модели мира. Моделировать подобный мир можно только с помощью математических формул, человек представить его просто не в состоянии. И здесь оказываются полезными невозможные фигуры. С философской точки зрения они служат напоминанием о том, что любые явления (в системном анализе, науке, политике, экономике и т. д.) следует рассматривать во всех сложных и неочевидных взаимосвязях.

Компьютерная графика на основе картины «Невозможный алфавит», 70х50 см, 1999 г.

Разнообразные невозможные (и возможные) объекты представлены на картине «Невозможный алфавит».

Третьей популярной невозможной фигурой является невероятная лестница, созданная Пенроузом. Вы будете по ней непрерывно или подниматься (против часовой стрелки) или спускаться (по часовой стрелке). Модель Пенроуза легла в основу знаменитой картины М. Эшера «Вверх и вниз» («Ascending and Descending»).

Существует еще одна группа объектов, реализовать которые не получится. Классической фигурой является невозможный трезубец, или «чертова вилка».

При внимательном изучении картинки можно заметить, что три зубца постепенно переходят в два на едином основании, что приводит к конфликту. Мы сравниваем количество зубцов сверху и снизу и приходим к выводу о невозможности объекта.

Невероятная лестница Пенроуза	«Чертова вилка»

Ресурсы Интернета о невозможных объектах

«Мир Эшера» («World of Escher»; http://www. worldofescher.com) — один из основных сайтов о Маурице Эшере, включающий галерею его работ и биографию.

Интересен сайт (на английском языке) Катерины Палмер (Catherine Leah Palmer; http://www.palmyra. demon.co.uk), состоящий из большой галереи невозможных фигур, в том числе анимированных. Здесь приведены работы основных художников «имп-арта».

Катерина Палмер также создала программу Illusionarium (http://www.palmyra.demon.co.uk/illusion/programs.htm) для построения невозможных фигур из кубиков. Программа имеет сложноватый интерфейс и ограниченное число комбинаций.

Impossible Puzzle 1.10

Сайт Влада Алексеева «Невозможный мир» (http://imp-world.narod.ru) включает большую галерею невозможных фигур, ссылки на художников и статьи о невозможных объектах (на русском языке). Автор сайта создал две интересные программы для построения невозможных объектов (их версии вы найдете на сайте) — Impossible Puzzle и Impossible Constructor (Freeware).

Системные требования:

• Процессор - Pentium 200 MГц
• Память - 64 Мбайт
• Место на жестком диске - 200 Кбайт
• Операционная система - Windows 95 с установленными библиотеками MFC 4.2, Windows 98/Me/NT/2000/XP.

Impossible Constructor

Программа предназначена для создания изображений невозможных фигур из элементарных треугольников путем складывания мозаики. Комбинируя треугольники, можно получить большое количество невозможных фигур. Программа имеет простой и понятный интерфейс.

Системные требования:

• Процессор - Pentium 100 MГц
• Память - 16 Мбайт
• Место на жестком диске - 200 Кбайт
• Операционная система - Windows 95 с установленными библиотеками MFC 4.2, Windows 98/ Me/NT/2000/XP.

Программа предназначена для конструирования изображений невозможных фигур из кубиков. В основе ее лежит та же идея, что и у программы Illusionarium Катерины Палмер, но в отличие от последней Impossible Constructor предоставляет полный набор из 64 кубиков, а также имеет более удачный интерфейс.

Сайт http://www. illusoria.com (на английском языке) включает целую галерею невозможных фигур.

* * *

Есть ли какая-либо более существенная польза от невозможных рисунков, чем игра ума? В некоторых больницах специально развешивают изображения невозможных объектов, поскольку их рассматривание способно надолго занять больных. Логично было бы развесить такие рисунки в кассах, в милиции и прочих местах, где ожидание своей очереди длится порой целую вечность. Рисунки могли бы выступить в роли этаких «хронофагов», т.е. пожирателей времени.

Об авторе
Дмитрий Раков — научный сотрудник РАН. Его рисунки вы найдете по адресу http://www.rakov.de.