Эксперимент №3: многоголовочные машины
Надежды на более эффективную и совершенную работу машин, как абстрактных, так и реальных, связаны с параллельной обработкой информации. Для абстрактных машин ей соответствует увеличение количества головок. Однако непонятно, как это повлияет на сложность программирования. Поэкспериментируем, введя в машины по одной дополнительной головке.
Многоголовочная МТ-программа (с учетом уже введенной адресации) (листинг 7):
Листинг 7. МТ-программа для машины с двумя головками
q1, 1[0]1[1], 0[2], q2 q2, 0[0], 1[2], q1 q2, 0[1], 1[2], q1
Легко видеть, что с двумя головками машина может анализировать по две ячейки в одной инструкции. Но существенно не это, а то, что качественно иным стал сам алгоритм. В данном случае он стал значительно короче и понятнее: если в состоянии q1 обе ячейки отмечены, то нужно обнулить выходную ячейку и перейти в состояние q2; если любая из ячеек в состоянии q2 не отмечена, то поставить единицу в выходную ячейку и вернуться в состояние q1. Такое описание гораздо ближе к исходной формулировке логической функции И—НЕ.
Кроме того, по сравнению с исходным вариантом программа уменьшилась почти в пять раз (с 14 инструкций до трех), число внутренних состояний сократилось почти в четыре раза (с семи до двух), а роль состояний обозначилась четче: q1 — внутреннее состояние, соответствующее единичному значению функции, q2 — нулевому. (Второе состояние необходимо для синхронизации параллельных процессов.)
Если введение дополнительной головки для МТ имеет явно положительный эффект, то с МП ситуация сложнее. Дело в том, что у МТ нет проблем с разветвлением алгоритма, т. е. с переключением из текущего состояния в любое другое, а у МП команда перехода разделяет вычислительный процесс только на две ветви. В случае же двух головок, или двух ячеек, мы имеем четыре ситуации, или четыре ветви (а в общем случае 2n ситуаций, где n — количество головок).
Следовательно, существующих возможностей команды перехода явно недостаточно. Если команда перехода МП будет анализировать не одну конкретную ячейку, а некоторую ситуацию, связанную с содержимым множества ячеек, то соответствующее логическое выражение будет иметь два значения — истинное и ложное.
Листинг 8. МП-программа для машины с двумя головками. 1-й вариант
1. ?(V[0]V[1]), 30, 21 2. ([2] 1 3. ? (( [0]), 40, 51 4. V[2] 1 5. ? (( [1]), 40, 21
Здесь ситуации, которые нужно анализировать в команде переходов, заключены в круглые скобки. Само значение ячеек ленты, составляющих конкретную ситуацию, стоит перед индексами. При этом символ V соответствует наличию метки на ленте, символ ξ — ее отсутствию. Теперь смысл команды перехода состоит в следующем: выполнить переход по первому адресу, если ситуация ложна, и по второму — в противном случае. Например, для первой команды программы ситуация истинна, когда в нулевой и первой ячейках есть метки.
Рассмотрев два варианта МП-программ для машины с двумя головками (листинги 8, 9), видим, что стало только хуже, так как размер МП-программы увеличился.
Листинг 9. МП-программа для машины с двумя головками. 2-й вариант
1. ?(V[0]V[1]), 3, 2 2. ([2] 1 3. V[2] 1
Более того, возникает необходимость оптимизации кода. Эта же проблема существенна и для МТ, но здесь ее решение качественно иного рода: для МТ оно сводится к минимизации конечных автоматов, для МП — к нахождению минимальной блок-схемы табличного задания алгоритма. О сложности решения последней задачи и ее неоднозначности достаточно подробно рассказано в [5]. Но если еще учесть, что МТ обобщает табличную форму задания алгоритмов, представляя любую таблицу переходов МТ-программой с одним состоянием, то на основе выводов из [5] следует, что в общем случае в «многоголовочном варианте» программы для МТ гораздо оптимальнее программ МП.
Эксперимент №4: использование внутренних состояний МТ
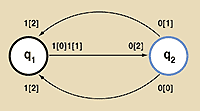
Рассмотрим графическое представление программ МТ. По форме это направленные графы, применяемые для описания конечных автоматов (рис. 4). Начальное внутреннее состояние МТ выделено жирным кружком, инструкциям перехода между состояниями МТ соответствуют дуги, соединяющие состояния, символ внешнего алфавита помечает начало дуги, такой же символ или символ перемещения головки помечает конец дуги.
Имена внутренних состояний МТ могут использоваться и для других целей, например вместо ячеек памяти (листинг 10, а также рис. 4).
Листинг 10. МТ-программа, использующая внутренние состояния
?0?, 1[0]1[1], - , ?1? ?1?, 0[0], - , ?0? ?1?, 0[1], - , ?0?
Примечание. В кавычки заключены имена внутренних состояний, соответствующие выходному значению функции.
Внутренние состояния можно использовать и в первом варианте МТ-программы (листинг 11).
Листинг 11. Исходная МТ-программа, использующая внутренние состояния
1. q50-q3, 2. q51Rq4, 3. q31Rq4, 4. q30-q3, 5. q41Lq5, 6. q40Lq3.
Примечание. Состояние q3 соответствует единичному значению функции, q5 — нулевому, q4 — промежуточное состояние.
Заметим, что в обоих случаях программы стали проще. Теперь нет нужды не только в перемещении головки, но и в действиях по изменению содержимого ленты (экономим еще и ячейки памяти!).
В применении внутренних состояний существует и своя специфика. Внешний наблюдатель может их в буквальном смысле «проморгать». В первом случае (листинг 10) в отличие от второго такой проблемы нет, так как программа «намертво» фиксирует текущее состояние до смены входной комбинации. Но, безусловно, эффект «мерцания состояний» нужно всегда учитывать.
Итак, не только адресация, но и использование внутренних состояний значительно уменьшает размер кода. Однако с введением символа «прочерк» появились инструкции, которые не изменяют внутреннее состояние машины и при этом не выполняют каких-либо действий (инструкция на листинге 11 под номером 4). Подобные инструкции вполне можно исключить из текста программы. Но если их убрать, то «истинная» машина Тьюринга должна остановиться! Чтобы этого не допустить, будем считать, что она функционирует, находясь в текущем состоянии до тех пор, пока не возникнет ситуация перехода в новое состояние. Безусловно, убранные инструкции можно легко восстановить. Этим соглашением мы исключаем избыточную информацию из программы, не особенно конфликтуя с теорией и законом функционирования абстрактной машины.
Обратите внимание, что отсутствие адресации ячеек привело к необходимости введения промежуточного состояния q4 — состояния анализа второй входной ячейки функции (см. листинг 11). И именно оно — источник «помех» или упомянутых «мерцаний» для выходного значения функции по отношению к внешнему наблюдателю. Более того, анализ показывает, что не только отсутствие адресации является причиной необходимости введения промежуточного состояния q4. Даже при использовании адресации ограничение на количество одновременно доступных символов в рамках одной инструкции вынуждает его вводить такое состояние. То есть и адресация ячеек, и увеличенное количество головок, наряду с использованием состояний, — необходимые условия значительного упрощения программирования МТ.
Современные процессоры и машины Поста и Тьюринга
Современные процессоры, как и большинство языков программирования, процедурны подобно модели Поста. Именно поэтому программист должен в явном виде определить последовательность исполнения инструкций в программе. Разная последовательность программных инструкций порождает разные программы, хотя конечный результат их работы один и тот же. На примере программ для МП это как раз и было показано.
При определении же алгоритма для МТ главное заключается не в фиксации последовательности выполнения инструкций, а в определении последовательности смены внутренних состояний. Инструкции выполняются в соответствии с условиями перехода из текущего состояния в новое состояние и, что замечательно, не зависят от порядка их записи в программе. В силу этого машина Тьюринга «умнее» машины Поста! Она непроцедурна.
Инструкции МТ ассоциативны и идентифицируются не своим номером или местом в памяти машины, а присвоенным им именем: именем внутреннего состояния, стоящим первым в инструкции.
Такая особенность МТ позволяет для хранения инструкций применять ассоциативную память (АП), которая намного эффективнее обычной памяти. Если в обычной памяти время выборки данных и инструкций зависит от их расположения в памяти (более длинные адреса требуют большего времени на дешифрацию), то для ассоциативной памяти такой проблемы не существует. В обычном же процессоре для большего объема памяти требуется больше разрядов для адресации ячеек памяти. Следствие этого — дополнительные аппаратные затраты.
Хоть АП и дорога, но ее применение оправданно, поскольку служит хранению управляющей структуры программ. Такой памяти нужно немного, и потому эффективность АП по отношению к стоимости весьма высока. Но ничто не мешает использовать АП и для хранения самих данных. Однако при этом объем АП будет определяться уже совсем другими факторами — сложностью системы команд и общей стоимостью машины.
Чтобы повысить скорость работы реальных процессоров, очень большое внимание уделяют проблеме предсказания команд. «Многообразие» программ МП демонстрирует сложность этой проблемы. Вот потому-то подобное «шаманство» и не приносит много пользы. У МТ такой проблемы нет. Для нее гораздо проще составить оптимальную программу, где все «предсказания» уже сосредоточены в ее тексте. А при наличии АП предсказание, как таковое, вообще теряет свой смысл!
Система прерываний процессора, параллелизм операционной среды и некоторые другие факторы сильно «ломают» современную базовую модель процессоров. Но на самом деле она остается по-прежнему фон-«постовской», а по сути, более известной под именем архитектуры фон Неймана. И даже такие «кардинальные» решения, как процессор Merced [4], по большому счету, какой-то новой модели не вводят.
Выводы
Хочется просто сказать: господа разработчики программных систем, обратите внимание на модель Тьюринга! Она использует иные принципы работы, которые при нынешнем уровне развития аппаратных решений легко реализуемы. А то, что они эффективны, мы уже убедились.
Набор операций, выполняемых абстрактными машинами, не говоря уж о типах данных, беден, но может быть довольно легко расширен. А вот управление остается фактически неизменным и при переходе к реальным проектам. Поэтому, изучая абстрактные машины, мы познаем наиболее универсальную «управляющую» часть алгоритмических моделей, а соответственно и средства, реализующие их, — аппаратуру и языки программирования.
Безусловно, МП и МТ не могут использоваться в чистом виде. Но не в этом их назначение: для многих практических решений они служат основой. Это следует из анализа аппаратных архитектур процессоров и большинства современных языков программирования, где базовой может считаться модель МП, а также из анализа методов и моделей, применяемых программистами в некоторых прикладных областях (например, проектирование компиляторов), где базовой может считаться модель МТ.
В связи с проблемами распараллеливания информационных потоков настало время вновь обратить свой взор на абстрактные машины. Дело в том, что так и нет общепризнанной параллельной модели, которая была бы сейчас или стала бы в перспективе основой для массовой универсальной параллельной процессорной архитектуры. Например, при рассмотрении архитектуры процессора Merced, который на такую роль претендует (или, пожалуй, претендовал?), основное внимание уделяется его аппаратным новшествам, а не его модели. Но в архитектуре процессора основное не сумма его блоков, а то, что их связывает, — модель. Та же проблема и с языками программирования. И здесь параллелизм — «узкое место».
Рассмотренные абстрактные машины не только подтверждают сказанное, но и подсказывают, в каком направлении необходимо двигаться, чтобы преодолеть имеющиеся трудности. Параллелизм — направление, в котором следует пытаться нарастить «мощь» любых абстрактных моделей, а не только рассмотренных. Этим необходимо заниматься, несмотря даже на то, что уже существуют специализированные «более молодые» параллельные модели (см., например, [7,8]). «Старый конь» не только «борозды не портит», но может и «глубоко вспахать». Как мы показали, у машины Тьюринга сил предостаточно. n
Литература
- Любченко В.С. Новые песни о главном-II // Мир ПК. 1998. № 7. C.112.
- Успенский В.А. Машина Поста. 2-е изд., испр. М.: Наука, 1988. 96 с. (Популярные лекции по математике).
- Катленд Н. Вычислимость. Введение в теорию рекурсивных функций: Пер. с англ. М.: Мир, 1983. 256 с.
- Кузьминский М. Вышел Merced из тумана // Computerworld Россия. 1997. № 47. C.31.
- Хамби Э. Программирование таблиц решений. М.: Мир, 1976. 86 с.
- Глушков В.М. Введение в кибернетику. К.: Изд-во АН УкрССР, 1964. 324 с.
- Питерсон Дж. Теория сетей Петри и моделирование систем: Пер. с англ. М.: Мир, 1984. 264 с.
- Краснов С.А. Транспьютеры, транспьютерные вычислительные системы и Оккам // Вычислительные процессы и системы / Под ред. Г.И. Марчука. Вып. 7. М.: Наука, 1990. 352 с.
