Структурная организация современных универсальных процессоров соответствует принципам, заложенным Джоном фон Нейманом еще в середине 1940-х годов. Но и сейчас основными блоками процессора по-прежнему остаются устройство управления (УУ), арифметико-логическое устройство (АЛУ), оперативное запоминающее устройство (ОЗУ), разнотипные устройства внешней памяти и т. п. Могли измениться название или структура устройства, а вот суть осталась прежней – «неймановской». Однако именно к изменению структуры процессора сводятся почти все непрекращающиеся попытки совершенствования процессорной архитектуры. Обычно это дублирование уже имеющихся узлов и создание между ними разнообразных дополнительных информационных связей.
Существует немало архитектур процессоров, основанных именно на структурной организации. Несмотря на то что структурных вариантов достаточно много, основные из них, имеющие практическую ценность, «обкатаны», а потому каких-то особых достижений на этом «поле» ожидать не приходится. Главная борьба пока ведется на уровне технологии производства кристаллов. Но есть другой путь. Это изменение существа процессора, или, говоря точнее, алгоритма работы его устройства управления.
В общих чертах алгоритм работы процессора при исполнении программ сводится к следующему:
1) установить начальный адрес программы в счетчике команд (СК);
2) загрузить по адресу, находящемуся в счетчике команд (СК), команду из ОЗУ в регистр команд (РК);
3) дешифровать команду: если это арифметическая команда, то выполнить ее и увеличить СК в соответствии с ее форматом; если логическая, то вычислить адрес следующей команды и поместить его в СК;
4) перейти к пункту 2.
Здесь в первую очередь следует обратить внимание на пункты 2 и 3. Манипулируя параметрами, указанными в этих пунктах (форматом команды, адресацией и т. п.), мы не только влияем на алгоритм работы процессора, но и фактически определяем его архитектуру.
Пока же получается, что структурная организация первична, а алгоритм вторичен. Это следует из того факта, что больше всего известны структурные классификации процессоров, а не алгоритмические. На самом же деле приоритет должен быть другим: структурный состав и организация процессора должны полностью определяться именно алгоритмом работы УУ. Или, что математически точнее, алгоритмическая модель, соответствующая выбранному классу вычислительных процессов, должна определять архитектуру процессора.
О формальных «корнях»
Для современных процессоров базовой можно считать алгоритмическую модель [1], подобную модели Поста [2]. В некоторых деталях она может меняться, иметь другое название (например, машина с неограниченными регистрами [3]), но суть та же: алгоритмы, реализуемые такими моделями, удобно изображать графически в виде так называемых блок-схем, являющихся эквивалентом текстовой формы программ.
Эксперименты, описанные ниже, применяют для представления и реализации алгоритмов другой алгоритмической модели или, как часто говорят, абстрактной машины. Причем такой машины, которая не только покрывает модель блок-схем (машину Поста), но и позволяет описывать практически любые алгоритмы (например, параллельные). Она перспективна и с точки зрения аппаратной реализации, поскольку мы все ближе подходим к достижению порога быстродействия элементной базы, в связи с чем возобновились активные поиски новых архитектур [4].
В данном случае знакомство с ними – отправная точка серьезных отношений с программными системами, а создание собственной абстрактной машины, если такое случится, – результат успешного их развития. И кто знает, возможно, мы и создадим машину, которая станет «абстрактным прообразом» будущих машин.
Именно такой путь мы и постараемся пройти. А так как конечной целью нашего путешествия будет абстрактная машина, базирующаяся на формальной модели конечного автомата, то мы и сравним широко известные абстрактные машины Поста и Тьюринга или аналогичные им алгоритмические системы с автоматной моделью программ [1]. Далее именно эти модели будут рассмотрены с точки зрения их автоматных свойств. При этом моделью, с которой мы собираемся больше всего экспериментировать и которую попробуем усовершенствовать, будет машина Тьюринга. В отличие от многих других моделей с автоматами ее роднит понятие внутреннего состояния.
Машина Поста
Прежде чем рассматривать и модифицировать машину Тьюринга, остановимся на машине Поста (МП) [2, 6]. Именно она более всего соответствует современным процессорам и языкам программирования. Уже только этим машина Поста привлекает к себе, так как, с одной стороны, демонстрирует эффективность и работоспособность идеи, которой уже более полусотни лет, с другой – ее рассмотрение и анализ дают понимание причин сложившегося застоя в развитии программных систем. Сегодня, например, весьма актуальной становится проблема распараллеливания процессов, которую с помощью машины Поста (да, кстати, и Тьюринга тоже) решить сложно или даже невозможно, особенно если манипулировать «чистыми» абстрактными машинами. Возможно, проблема параллелизма во времена их создания была не столь актуальной, как ныне, а потому при их «изобретении» и не учитывалась.
|
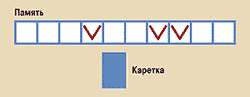
| Рис. 1. Машина Поста |
Машина Поста состоит из памяти и устройства управления, которое, следуя современной терминологии, будем называть процессором (рис. 1). Память в машине представлена разбитой на ячейки (клетки) бесконечной, или неограниченно растущей в обе стороны, лентой. Ячейки пронумерованы целыми числами ..., -3, -2, -1, 0, 1, 2, 3... Каждая ячейка может быть либо пустой, либо обозначенной меткой (например, V). Метке может соответствовать и запись в ячейку значения нуля или единицы.
Процессор изменяет информацию на ленте с помощью специальной каретки [2], выполняя при этом команды, упорядоченное конечное множество которых составляет программу его работы. Состав этих команд следующий:
Команда движения вправо:
i. => j
Команда движения влево:
i. => j
Команда печатания метки:
i. V j
Команда стирания метки:
i. н? j
Команда передачи управления:
i. ? j10, j21
Команда остановки:
i. стоп.
Здесь i б- номер команды, а число, стоящее в конце команды, отсылка, т. е. номер или адрес следующей выполняемой команды.
Набор команд МП прост, и их функциональное назначение в основном понятно. Поясним лишь команду передачи управления. Она передает управление команде с номером j10, если содержимое ячейки пусто, и j21 – если нет.
Для изучения свойств МП рассмотрим в качестве примера программу реализации или моделирования логической функции Иб-НЕ (листинг 1). Алгоритм ее работы включает в себя анализ двух соседних ячеек (входных ячеек) и изменение третьей ячейки (выходной ячейки). Если входные ячейки отмечены, то в выходной метка стирается; если хотя бы в одной из входных ячеек метка отсутствует, то в выходной ячейке метка ставится.
Листинг 1. МП-программа моделирования И–НЕ
1. ?, 2б?, 71 2. => 3 3. => 4 4. V 5 5. <= 6 6. <= 1 7. => 8 8. ?, 3б?, 91 9. => 10 10. н? 5
|
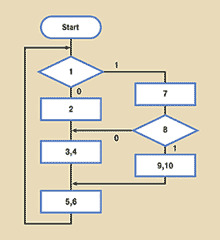
| Рис. 2. Блок-схема алгоритма логической функции Иб-НЕ |
Графическая форма программы представлена на блок-схеме (рис. 2), внутри элементов которой проставлены номера команд программы. Блок-схема нагляднее листинга программы отражает некоторые особенности работы алгоритма. В данном случае четко видна «цикличность» и «бесконечность» алгоритма.
Уже на основе этого простого примера просматривается связь между современными реальными процессорами и языками их программирования, а также данной машиной и языком ее программирования. При этом графическая форма полностью соответствует форме блок-схем современных программ, а командам абстрактной машины можно подобрать аналоги среди программных инструкций реальных языков программирования.
Листинг 2. Программа моделирования И–НЕ на Си
int x[3]; int n = 1; m1: if (!x[n]) goto m2; else goto m7; // первый вход m2: n++; goto m3; m3: n++; goto m4; m4: x[n] = 1; goto m5;// выход = 1 m5: n-; goto m6; m6: n-; goto m1; m7: n++; goto m8; m8: if(!x[n]) goto m3; else goto m9; // второй вход m9: n++; goto m10; m10: x[n]=0; goto m5;// выход =0
В программе на языке Си (листинг 2) лента абстрактной машины моделируется массивом целых чисел (x); номерам команд МП-программы соответствуют метки программных инструкций; команды перемещения вдоль ленты реализуются изменением значения индекса массива (n); переход к соответствующей инструкции б- командой goto; команды передачи управления б- инструкцией if.
Машина Тьюринга
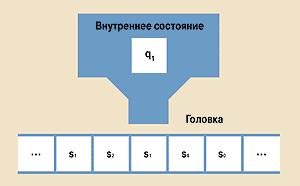
Теперь рассмотрим машину Тьюринга (МТ) [3,6]. Она структурно аналогична МП и тоже состоит из памяти и процессора. Память в данном случае представляет собой бесконечное, как и в случае ленты у МП, множество ячеек (рис. 3). Здесь в каждую ячейку может быть записан один из символов конечного множества s0, s1, s2, ..., sn, называемого внешним алфавитом МТ, где символ s0 соответствует пустому содержимому ячейки памяти.
|
| Рис. 3. Пример машины Тьюринга |
Процессор представляет собой дискретное управляющее устройство, которое может находиться в одном из своих внутренних состояний, обозначенных символами q1, q2, ..., qm. У него имеется головка, обозревающая в каждый момент времени только одну ячейку памяти МТ.
Действия процессора МТ зависят от его текущего внутреннего состояния и того символа, который обозревается головкой в рассматриваемый момент времени. Множество инструкций составляют программу МТ. При этом каждая инструкция в соответствии с типами операций принадлежит множеству вида:
1. 1. qisjskql
2. 2. qisjRql
3. 3. qisjLql
В первом случае МТ, находясь в состоянии qi и имея на входе головки символ sj, заменяет его символом sk, после чего переходит в новое состояние ql. Во втором и третьем случаях машина не изменяет содержимое ячеек памяти, а только передвигает головку на одну позицию вправо или влево от текущего положения. Множество символов внутренних состояний и символы R, L (движение головки влево, вправо) составляют в сумме так называемый внутренний алфавит машины.
Рассмотрим программу для МТ, аналогичную уже описанной программе для машины Поста. Текст МТ-программы (листинг 3) и логика ее работы достаточно сильно отличаются от принципов, являющихся основой современных языков программирования, а соответственно и архитектуры процессоров.
Листинг 3. МТ-программа моделирования И–НЕ
1. q10Rq2, 2. q11Rq4, 3. q20Rq3, 4. q21Rq3, 5. q301q6, 6. q311q6, 7. q40Rq3, 8. q41Rq5, 9. q500q6, 10. q510q6, 11. q61Lq7, 12. q60Lq7, 13. q70Lq1, 14. q71Lq1.
В то же время понятно, что внутренние состояния МТ в явной форме отражают процесс, присущий неявно МП. В данном случае роль внутренних состояний следующая: q1 б- начальное состояние машины и состояние анализа нулевой ячейки ленты; q2, q4 б- состояния анализа первой ячейки; q3 б- состояние установки третьей ячейки, или выходного значения функции в единицу; q5 б- состояние установки третьей ячейки или выходного значения функции в ноль; q6, q7 б- состояния последовательного возврата головки к нулевой ячейке ленты и в начальное состояние q1.
Приведенная программа для МТ, имея то же множество символов внешнего алфавита и во многом аналогичный набор команд, что и МП, почти в полтора раза длиннее МП-программы. Всегда ли и в силу чего это так? Можно ли что-то сделать, чтобы ситуация была иной? Зная ответы на поставленные вопросы, мы поймем, существуют ли эффективная и удобная для программирования архитектура процессоров и язык программирования, основанные на других формальных алгоритмических моделях. Для этого нужно попытаться упростить запись МТ-программ, сделав их более ясными и читабельными с сохранением, конечно, присущих им положительных качеств.
Эксперимент б№1: символ «прочерк»
Детальное сравнение программ МП и МТ показывает, что в первом случае, чтобы передвинуть головку на одну позицию, достаточно одной команды, а во втором – нужно обязательно проанализировать символ. В силу этого МТ для безусловного сдвига и изменения информации на ленте (безусловного б- значит, независимого от значения символа) требуется число команд, пропорциональное числу символов внешнего алфавита. А так как то или другое необходимо время от времени делать, требуемое количество команд в этих случаях для МТ больше.
Чтобы устранить этот недостаток, дополним внешний и внутренний алфавиты МТ символом «прочерк». Он будет соответствовать всем символам соответствующего алфавита МТ (внутреннего или внешнего). Мы поместим его в позицию соответствующего символа команды. Это будет вторая позиция, если нужно провести безусловные операции перемещения или записи нового символа в текущую позицию на ленте, и третья, когда не нужно проводить операций с лентой. Кстати, если символ «прочерк» поставить в обеих этих позициях, то просто изменится внутреннее состояние машины – безусловное изменение внутреннего состояния.
С учетом этого программа моделирования И–НЕ.
Листинг 4. МТ-программа, использующая символ «прочерк»
1. q10Rq2, 2. q11Rq4, 3. q2-Rq3, 4. q3-0q6, 5. q40Rq3, 6. q41Rq5, 7. q5-1q6, 8. q6-Lq7, 9. q7-Lq1.
Данная программа станет даже короче, чем аналогичная для МП! Сокращение произойдет за счет замещения «парных» инструкций одной. При этом само множество внутренних состояний программы и их роль остаются прежними. Таким образом, расширив внешний алфавит машины символом «прочерк», мы успешно решили задачу упрощения МТ-программ.
Рассмотрим ситуацию, когда команды МТ удобнее команд МП. Можно заметить, что одной команде МТ, которая изменяет символ в ячейке, соответствуют несколько команд МП. Например, команде МТ, заменяющей 0 на 1:
q101q2
соответствует следующий фрагмент команд МП:
n. ?, n+1, n+2
n+1. V, n+2
n+2. ...
В этом случае команда МТ одновременно проверяет текущий символ на соответствие определенному значению и изменяет его на новое значение. У МП эти же действия выполняются с помощью двух команд: команды проверки и команды изменения символа, что справедливо для использования двоичного алфавита. В общем же случае из-за того, что символы внешнего алфавита нужно представить в двоичном коде, МП требуется уже более двух команд. Этот код нужно распознать и, распознав, заменить другим кодом. Но так или иначе это фрагменты из нескольких команд. И чем «шире» код, тем большее количество команд будет входить в эти фрагменты. Но справедливости ради заметим, что реальные машины распознают символы гораздо успешнее, так как могут работать с множеством битов б- байтами, словами и т. п.
Эксперимент б№2: адресация ячеек ленты
В реальном процессоре аналогом ленты является память. Он не «скрипит», перемещая головку, а работает с памятью подобно тому, как программист работает с одномерным массивом. При этом индекс элемента массива соответствует адресу или номеру ячейки на ленте.
С применением индексации, а по существу, адресации ячеек ленты рассмотренные ранее примеры программ примут иной вид (листинг 5, 6).
Листинг 5. МП-программа, использующая адресацию
1. ?[0], 2, 3 2. V[2] 1 3. ?[1], 2, 4 4. н?[2] 1
Примечание. В квадратных скобках указан адрес текущей ячейки на ленте и индекс элемента массива ячеек памяти (ленты).
Листинг 6. МТ-программа, использующая адресацию
q1, 0[0], 1[2], q2 q1, 1[0], -, q2 q2, 0[1], 1[2], q1 q2, 1[1], 0[2], q1
Примечание. В программе убраны номера инструкций (для МТ в них нет особого смысла), и разделены запятыми элементы инструкции. Заметим, что символ «прочерк» включен и во внутренний алфавит машины. В этом случае он отражает уже отмеченную ранее ситуацию, когда нет необходимости в выполнении каких-либо действий по изменению ячеек памяти.
Адресация значительно сократила размер программ, устранив как рудимент необходимость в перемещении каретки/головки. Но хотелось бы знать, как «нововведение» скажется на теории машин. Скорее всего, хуже не будет. Адресация не является для абстрактных машин чем-то необычным. Пример этого б- машина с неограниченными регистрами (МНР) [3]. У нее регистр б- это ячейка памяти, а его номер б- адрес или индекс массива в памяти.
Литература
- Любченко В.С. Новые песни о главном-II//Мир ПК. 1998. б№7. с.112.
- Успенский В.А. Машина Поста. 2-е изд., испр. М.: Наука, 1988. 96 с. (Популярные лекции по математике).
- Катленд Н. Вычислимость. Введение в теорию рекурсивных функций: Пер. с англ. М.: Мир, 1983. 256 с.
- Кузьминский М. Вышел Merced из тумана//Computerworld Россия.1997. б№47. С.31.
- Хамби Э. Программирование таблиц решений. М.: Мир, 1976. 86 с.
- Глушков В.М. Введение в кибернетику. Киев: Изд-во АН Укр ССР. 1964. 324 с.
- Питерсон Дж. Теория сетей Петри и моделирование систем: Пер. с англ. М.: Мир, 1984. 264 с.
- Краснов С.А. Транспьютеры, транспьютерные вычислительные системы и Оккам//Вычислительные процессы и системы / Под ред. Г.И. Марчука. Вып. 7. М.: Наука., 1990. 352 с.
