д. Римская цифра в имени возрастала на единицу всякий раз, когда качество программы существенно улучшалось. Последняя, V, продержалась очень долго, свидетельствуя о первенстве (Victory) продукта среди аналогичных. Теперь же после слова Maple производители поставили арабскую цифру, чтобы сообщить о появлении качественно нового продукта. Так чем же замечательна эта версия Maple?
Стратегическая инициатива
Многое восхищало в программе Maple V: простой и удобный интерфейс, способность мгновенно вычислять и упрощать громоздкие математические выражения, высокое полиграфическое качество формул и великолепная двух- и трехмерная графика. Число зарегистрированных пользователей программы перевалило за миллион. Однако для проведения трудоемких численных расчетов с большими массивами данных производительность программ на встроенном языке Maple была недостаточна высока, и потому приходилось применять дополнительные средства, такие как компиляторы Си и Фортран. И тогда разработчики Maple решили существенно повысить производительность численных расчетов. Для этого компания Waterloo Maple заключила стратегически важное и очень своевременное соглашение с признанным мировым лидером в области разработки численных алгоритмов фирмой NAG о совместной разработке новой версии продукта под названием Maple 6. В результате двухлетней работы программа Maple пополнилась новым пакетом матричных расчетов LinearAlgebra, где были применены соответствующие алгоритмы компании NAG. Команды пакета LinearAlgebra во многом повторяют команды входившего в предыдущие версии Maple пакета linalg, который, видимо, будет исключен.
Сравнение скоростей матричных вычислений программ Maple, Matlab и Mathematica
Оценить производительность продуктов Maple, Matlab и Mathematica можно на взятом из программы Mathematica примере вычисления собственных значений случайной матрицы 1000х1000 и построения графика их абсолютных величин (рис. 1).
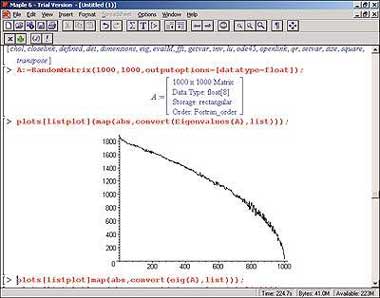 |
| Рис. 1. График абсолютных величин собственных значений случайной матрицы размером 1000х1000 |
Решение этой задачи в программе Mathematica на компьютере с Celeron-366 и оперативной памятью 64 Mбайт заняло 3 мин 42 с. Программный процессор Matlab 5.3.1, вызываемый из Maple с помощью встроенного пакета Matlab, справился с ней за 3 мин 39 с, а вот новый пакет LinearAlgebra программы Maple 6 затратил на это 3 мин 22 с. Таким образом, производительность Maple 6 при выполнении этого примера оказалась выше, чем у Matlab, приблизительно на 10%.
По данным разработчиков, такие матричные операции, как умножение и LU-разложение при размере матрицы выше 200х200, делаются в Maple (с помощью команд пакета LinearAlgebra) в несколько раз быстрее, чем соответствующими командами в среде Matlab или Mathematica.
Матричные графики
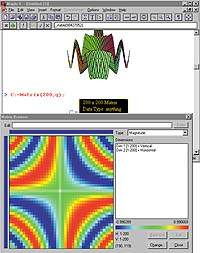 |
| Рис.2. Матричный браузер позволяет оценить численные значения элементов массива |
Быстрое выполнение расчетов с большими массивами данных дает возможность использовать Maple для обработки сигналов и изображений, при математическом моделировании сложных систем и решении различных технических задач. А для наглядного представления больших массивов данных в программу добавлены соответствующие средства визуализации.
Появился так называемый матричный браузер, позволяющий оценивать численные значения элементов матрицы, диапазон и неравномерность распределения. Теперь матрицы размером более 10х10 не выводятся на экран, а выcвечивается лишь общая информация о них (рис. 2). С помощью контекстного меню, появляющегося на экране после нажатия правой кнопки мыши, можно вызвать матричный браузер или использовать одну из команд пакета LinearAlgebra для преобразования матрицы.
Maple как приложение MS Excel
Если на компьютере установлена электронная таблица Excel 2000, то после инсталляции программы Maple 6 вы обнаружите в меню Сервисб?Надстройка в списке подключаемых к Excel дополнений и строку Maple 6 Excel Edd-in. Если активизировать ее (отметив галочкой), то из Excel автоматически станут доступны все команды Maple. Они будут представлены в виде панели, имеющей кнопки для вызова справки, разюясняющей правила работы, команды и функции. Кроме того, пользователи могут подключать и отключать специализированные пакеты и программы собственной разработки.
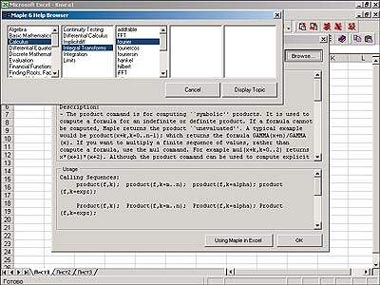 |
| Рис.3. Maple Excel link – так можно выбрать команду Maple из браузера и прочитать ее описание |
Следует отметить, что основная программа при этом не запускается, а подключаются только необходимые dll-библиотеки.
По сути, средство подключения Maple к Excel выполняет те же функции, что и приложение Mathematica Excel link или Matlab Excel link. Однако Maple Excel link распространяется вместе с Maple совершенно бесплатно, как, впрочем, и другие ее приложения, а вот в конкурирующих программах – как отдельный продукт, причем за весьма немалую плату.
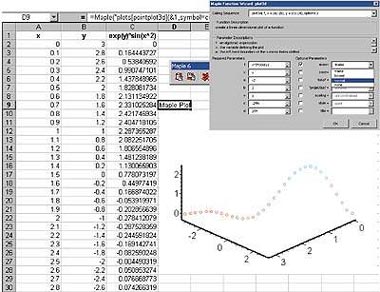 |
| Рис.4. Трехмерный график Maple на рабочей странице Excel |
На рис. 4 в качестве примера показано, как можно с помощью Maple Excel link построить график пространственной кривой по данным, введенным в таблицу Excel. Интерактивный диалог позволяет настроить параметры его вывода.
Графика в Maple 6
Браузер данных
Как уже упоминалось выше, большие массивы, матрицы и векторы теперь не выводятся на экран. Для их визуализации используется матричный браузер, дающий возможность представить информацию в режиме:
- цветовой амплитуды (рис. 2), когда цвет ячеек изменяется в зависимости от величины числа от синего к красному;
- структуры, когда черным цветом выделяются все ячейки таблицы, содержащие данные;
- плотности, когда в черно-белом изображении степень черноты ячейки пропорциональна абсолютной величине записанных в ней данных.
Чтобы просмотреть или изменить какие-либо значения данных, можно развернуть на весь экран определенный участок таблицы (рис. 5).
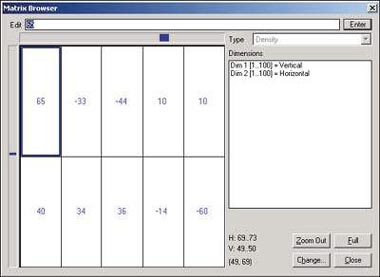 |
| Рис.5. Так можно просмотреть и изменить отдельные значения данных в матричном браузере |
Форматы графических обюектов
Графики, полученные в Maple, можно сохранить (либо экспортировать) в графические форматы DXF, JIF, EPS, JPEG/JPG, POV, WMF, BMP. Для экспорта картинки достаточно вызвать контекстное меню на графике и из его пункта Export as выбрать нужные формат и каталог для сохранения. К графическим улучшениям относятся, кроме того, возможность подключения и редактирования легенды для кривой (или нескольких кривых) на двухмерных графиках, а также изменения размера символов в точечных графиках. В пакете plots появилась команда matrixplot для построения трехмерной поверхности по значениям матрицы.
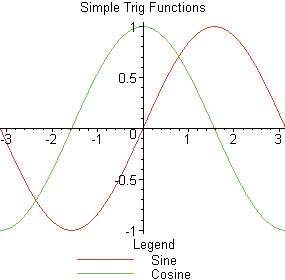 |
| Рис.6. Подключаемая и редактируемая легенды на двухмерном графике |
Языковые и системные изменения в Maple 6
Вызов и подключение внешних процедур
Это одно из наиболее существенных улучшений программы Maple 6, поскольку позволяет неограниченно расширять ее возможности за счет внешних приложений. Процедуры, написанные на языке Си или любом другом, имеющем Си-интерфейс, которые найдены в библиотеках расширений (DLL в Windows), могут подключаться к Maple в процессе и затем вызываться как собственные Maple-процедуры.
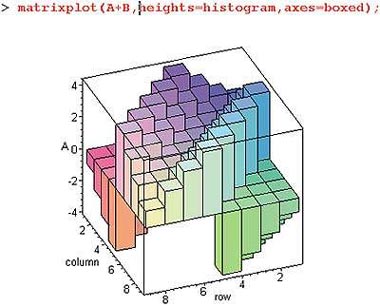 |
| Рис.7. Трехмерный матричный график |
С целью обюединения или изоляции соответствующих данных и процедур их обработки введены новые обюекты – модули, а также необходимые ключевые слова, языковые конструкции и функции для их обслуживания. Новый пакет LinearAlgebra тоже был добавлен в программу в качестве модуля.
Теперь на 32-разрядных компьютерах обюекты могут иметь 226-1 членов в одном выражении вместо 217-1, и значит, полиномы могут включать около 33 млн. членов, а не 60 тыс.
Небольшие целые числа (со значением менее 230 на 32-разрядных машинах или 262 на 64-разрядных) стали сохраняться в памяти более эффективно, что ускоряет расчеты и уменьшает обюем используемой оперативной памяти.
Символ конкатенации двух обюектов в конструкциях встроенного языка изменен: ранее использовалась точка, а сейчас – пара вертикальных линий. Точка же применяется для матричного и векторного умножения.
Конечный разделитель для утверждения if был ранее fi, для циклов – od, а для процедур – end. В новой версии Maple ключевым словом end может заканчиваться любая структура. Оно является корректным и по умолчанию может сопровождаться начальным разделителем структуры. Таким образом, if-структура может оканчиваться как словом end, так и словосочетанием end if. Цикл (for..while..do) может заканчиваться и end и end do, и т. д. Для обратной совместимости ключевые слова fi и od сохранены.
Изменения в численных расчетах
Для тщательного контроля численных расчетов Maple 6 выполняет естественное расширение до произвольной точности и точной арифметики стандартов IEEE-754 и IEEE-854.
Ядро Maple 6 было усовершенствовано так, что комплексные числа представляются собственными структурами данных. Это ускорило выполнение вычислений с комплексными числами.
Пакеты, исключенные из программы, а также новые и улучшенные
Из программы устранен пакет logic, а функции удаленного пакета totorder полностью переданы команде assume. Добавлен пакет LinearALgebra, самый значительный в новой версии. Точность, аккуратность, надежность, производительность его функций, а также принцип построения в среде Maple теперь станут примером для последующего улучшения и изменения всех имеющихся и вновь разрабатываемых программ для численных расчетов.
Пакет Slode
Этот пакет содержит функции для нахождения решений обыкновенных дифференциальных уравнений (ОДУ) в виде степенных рядов (гипергеометрических, полиномиальных, рациональных и разреженных).
Средства для полиномов (polytools)
Этот пакет обюединил множество команд Maple, ранее использовавшихся для вычислений с полиномами, таких как minpoly, recipoly, split, splits и translate, добавлены также и некоторые другие команды. Появился и пакет Spread, обеспечивающий программируемый доступ к электронным таблицам Maple. Он включает команды для преобразования данных в отдельных ячейках или блоках с использованием матриц.
Был улучшен подпакет Rif пакета Detools, представляющий собой мощный набор команд для упрощения и анализа систем полиномиально-нелинейных дифференциальных уравнений, обыкновенных и в частных производных.
Алгебраические кривые (algcurves)
Были добавлены пять новых функций.
Символьные вычисления
Решатель обыкновенных дифференциальных уравнений dsolve содержит реализации большинства известных способов решений, включая эвристические методы. Maple 6 был пополнен новыми алгоритмами с учетом новых публикаций и замечаний пользователей. В результате большинство внутренних шагов вычисления, используемых командой dsolve, стали доступны на уровне пользователя, включая все методы интегрирования и симметрии. Новые, необязательные параметры в команде dsolve позволяют применять выбранные методы расчета, что помогает понять различные возможные процедуры решения.
Теперь можно решить ОДУ или систему таких уравнений при наличии ограничений, которые могут быть заданы как уравнения или неравенства и могут включать как зависимые переменные, так и другие введенные функции либо символы.
В пакет были добавлены новые методы, а некоторые устаревшие были заменены более эффективными. Примеры из известной монографии Камке были решены на 97%. Дополнительно включены методы решения ОДУ сравнением с инвариантными семействами ОДУ (как предложено в Computer Physics Communications, б№113 (1998), p. 239) и решение ОДУ Абеля методом, опубликованным в статье «Equivalence and New Integrable Classes», появившейся в упомянутом журнале в этом году.
Обыкновенные дифференциальные уравнения второго порядка
Для решения нелинейных ОДУ второго порядка были использованы недавно опубликованные новые методы. Теперь стало возможным решать 95% задач из монографии Камке.
Новые методы также были включены для решения дифференциальных уравнений выше второго порядка – стало возможным распознавание в уравнении высокого порядка кратной производной от линейного уравнения первого порядка, интегрирующих полиномиальных множителей, а также решаемости методами симметрии.
Алгоритмы решения систем ОДУ были переписаны с целью использования преимуществ пакета diffalg и подпакета Rif.
Среди наиболее важных новшеств следует отметить:
- возможность включать в систему алгебраические уравнения и неравенства;
- возможность разбивать одно решение на несколько в соответствии с величинами или соотношениями между функциями либо символами, включенными в систему в качестве параметров;
- более эффективные методы решения ОДУ и более простой ответ, а также возможность задания предпочтительного порядка решения.
- упрощение нелинейных систем ОДУ, что приводит как к значительному расширению типов решаемых систем, так и к упрощению ответов по сравнению с версией 5.0.
Новые алгоритмы были применены в пакете pdsolve для решения линейных и нелинейных уравнений в частных производных. Для уравнений второго порядка pdsolve теперь пытается разложить дифференциальный оператор на множители, что позволило решать многие уравнения, с которыми не справлялась версия 5.0.
Появившаяся в пакете PDEtools команда casesplit позволяет анализировать и упрощать PDE-системы и в то же время ищет различные способы разделения переменных в уравнениях или системах. Еще одна новая команда в пакете PDEtools, separability, дает возможность определить, когда заданное уравнение допускает решение разложением на сумму или произведение. Если separability используется вместе с командой casesplit, то определяются практически все случаи, в которых уравнение может быть решено разделением переменных, и тогда задача сводится к решению уравнений, полученных разделением переменных.
Изменились и решатели Maple. Команда discont теперь знает почти обо всех разрывах специальных функций и возвращает их значения, например, при
> discont(ln(exp(I*x)), x); Ошибка! Неизвестный аргумент ключа. возвращаются все целые множители числа о?
Команда isolve может решать в поле целых чисел и некоторые неравенства, что ранее ей не удавалось.
Хорошо известно, что в общем случае корни полиномов пятой степени не могут быть найдены в радикалах. Новая Maple знает все случаи решения этих полиномов и выписывает соответствующее аналитическое решение при использовании команды solve.
Существенно улучшена и команда simplify, особенно когда она используется для выражений со специальными функциями. Команда convert теперь преобразует тригонометрические выражения в радикалы, когда аргументы кратны 0, о?/6, о?/4, о?/3, о?/2 или о?, а функция expand уже может раскладывать в сумму тригонометрические функции Якоби и Вейерштрасса.
Команда minimize (нахождение минимума) была полностью обновлена – она возвращает не только минимум, но и значение независимой переменной, при которой найден минимум, путем добавления опции location=true.
Поскольку стали применяться не только численные методы нахождения минимума, но и (если это возможно) аналитические, значительно расширился класс выражений, которые можно решать с помощью команды minimize.
Усовершенствование интерфейса в Maple 6
В новом варианте интерфейса стало возможным:
- производить автоматически все замены, а не только последовательные, как было раньше;
- импортировать и экспортировать данные в форматах Matlab, MatrixMarket или Tab Delimited;
- организовывать поименованные электронные таблицы. В дальнейшем эти имена могут быть изменены;
- осуществлять программный доступ, а также преобразование таблиц и данных в них из командной строки Maple 6 (позволяет программам и функциям создавать и преобразовывать таблицы в рабочих страницах);
- использовать редактор гиперссылок для одновременного введения адреса во всех гиперссылках или при наборе гиперссылок рабочего листа.
- экспортировать рабочие листы Maple в формат RTF для использования их в Word 2000 и во всех ОС Windows, поддерживающих Word 2000;
- указывать минимальный размер страниц и печатать их номера;
- прятать или показывать при выводе на экран электронные таблицы, Maple-ввод и вывод, графики;
- использовать два размера кнопочных палитр, причем один из них в полтора раза больше основного;
- вводить команду на создание матрицы при помощи матричной кнопочной палитры.
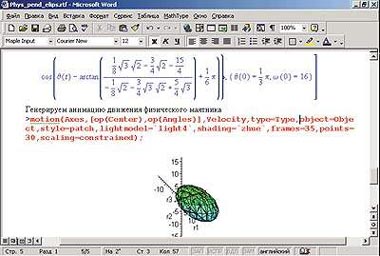 |
| Рис. 8. Так выглядит в интерфейсе Word 2000 экспортированный из Maple 6 файл в RTF-формате |
Заключение
До некоторого момента времени все программы математических расчетов можно было разделить на две категории. В одну входят программы численных расчетов, расширяющие возможности языков программирования высокого (или сверхвысокого) уровня. Они включили в себя лучшие алгоритмы численных расчетов. К ним следует отнести в первую очередь пакет Matlab компании Mathworks, сравнительно недавно появившийся пакет Gauss компании Aptech, а также свободно распространяемый Scilab. В каком-то смысле библиотеки численных алгоритмов компании NAG, расширяющие возможности языков высокого уровня Си и Фортран, также попадают в эту категорию.
Другая категория – программы аналитических расчетов, или системы компьютерной алгебры, позволяющие получать решение в точном аналитическом виде. К их числу можно отнести как программы Derive и Reduce, так и первые версии продуктов Maple и Macsyma.
Системы численных расчетов больше приспособлены для создания независимых приложений, включая разработку интерфейса. А вот в программах компьютерной алгебры для лучшего восприятия аналитических выкладок особое внимание уделяется полиграфическому оформлению формул, и потому они больше подходят для создания научных документов, в том числе «электронных книг» с «живыми» (перевычисляемыми при изменении данных) формулами.
Лучшие программы обеих категорий поддерживаются практически на всех широко используемых платформах, используют превосходную двух- и трехмерную графику, позволяют выполнять большое количество расчетов в интерактивном режиме, не прибегая к дополнительному программированию, и в то же время обладают мощными средствами для последнего. Некоторые функции и возможности присущи продуктам как той, так и другой категории. Например, одно из приложений программы Matlab – символьная библиотека программы Maple, а программы компьютерной алгебры содержат, в свою очередь, алгоритмы численных расчетов.
Тенденция к включению функций продуктов обеих категорий, т. е. к универсальности проявляется и в последних версиях программ математических расчетов. Например, сравнительно недавно появилась программа Mathematica компании Wolfram Research, которая изначально была задумана как универсальный математический пакет.
Несколько особняком стоит программа Mathcad компании Mathsoft, обладающая широкими сервисными и функциональными возможностями. Однако она имеет весьма ограниченные средства программирования, уступает по производительности расчетов и качеству графики и работает только под управлением Windows. Поэтому Mathcad скорее можно назвать мощным научным калькулятором, а не математическим программным продуктом.
Хотя последние версии программ Maple и Mathematica уже называют универсальными математическими пакетами, до сих пор не появилось такой программы, которая одинаково хорошо выполняла бы функции, присущие лидерам обеих категорий. С другой стороны, Matlab, один из лучших пакетов для выполнения численных расчетов, начал развиваться как набор специализированных приложений. Сейчас насчитывается более 50 так называемых тулбоксов, подключаемых к Matlab и значительно расширяющих его функции в различных областях. Кроме того, большое количество специальных приложений этого ПО разрабатывается и распространяется сторонними производителями. Поскольку в настоящее время догнать Matlab по широте приложений какая-либо другая программа вряд ли сможет, универсальный математический пакет, на мой взгляд, должен включать Matlab как основную составляющую численных расчетов.
 |
| Рис. 9. Пример использования пакета Slode – нахождение решения дифференциального уравнения в виде формального гипергеoметрического ряда |
Появление пакета Matlab в версии Maple V 5.0 многие восприняли как знак сближения усилий компании Waterloo Maple, занимающейся ПО для аналитических расчетов, и фирмы Mathworks, разрабатывающей продукты для численных расчетов, в деле создания универсального математического пакета. К тому же пакет Maple для символьных расчетов уже давно стал одним из тулбоксов Matlab. Однако Waterloo Maple предпочла работать с другим партнером – компанией NAG, специализирующейся на поставке библиотек алгоритмов численных расчетов. Время покажет, насколько правильным был выбор такой стратегии.
Первые тесты нового детища Waterloo Maple позволили сделать вывод о том, что по производительности матричных вычислений Maple уже сравнялась с программой Matlab и даже в некоторых случаях превзошла ee.
Таким образом, можно заключить, что сделан еще один большой шаг в совершенствовании универсального математического пакета: появилась новая версия Maple 6, которая по производительности и функциональности значительно обогнала своего ближайшего соперника – программу Mathematica.
ОБ АВТОРЕ
Борис Манзон – к. ф.-м. н., менеджер по научному программному обеспечению компании SoftLine
