В случае с вычислительными сетями известный постулат "время - деньги" звучит так: "скорость влетает в копеечку". Как рассчитать необходимую скорость канала связи, исходя из параметров локальной сети?
В последнее десятилетие число установленных локальных сетей увеличивалось с какой-то невообразимой скоростью. Сегодня сетевая рабочая станция - настолько же непременная принадлежность любого офиса, как, в свое время, пищущая машинка. По мере расцвета локальных сетей организации стали задумываться о том, как связать их между собой в сети глобальные. Сначала появились локальные мосты, потом - маршрутизаторы и мосты между удаленными друг от друга сетями. Тут уже понадобились средства связи для передачи информации от одной точки к другой.
Перед любым администратором, планирующим реализацию такой глобальной сети, с неизбежностью встает проблема выбора скорости передачи данных между связываемыми локальными сетями. Поскольку ежемесячная плата за цифровой канал обычно пропорциональна скорости передачи, завышение необходимой пропускной способности ведет к непроизводительным расходам средств. Помимо этого, выбрав линию с недостаточной пропускной способностью, администратор сети непременно навлечет на себя недовольство со стороны пользователей - канал не сможет обеспечить требуемые скорость и качество связи между локальными сетями.
Даже если администратор решит облегчить себе задачу, обратившись к использованию таких сетевых служб, как frame relay, это все равно не избавит его от необходимости выбрать оптимальную скорость работы канала между локальной сетью и сетью frame relay. Решение придется принимать и относительно CIR (Committed Information Rate).
Попытки обратиться за помощью к справочной литературе не слишком приблизят к решению задачи выбора подходящей скорости работы глобальной сети. В книжках обычно пишут, что пропускная способность канала должна быть не меньше 56 Кбит/c; некоторые подозрения, однако, вызывает полное отсутствие информации о зависимости между интенсивностью трафика по глобальной сети и пропускной способностью каналов связи. Возникает также резонный вопрос: неужели 56 Кбит/c так уж необходимы для организации самого примитивного межсетевого обмена информацией, например пересылки текстовых сообщений по электронной почте?
Короче говоря, выбор оптимальной скорости работы глобальной сети - интересная задача, имеющая большое практическое значение. В данной статье рассказывается о том, как можно применить математический аппарат теории массового обслуживания для оптимизации скорости передачи в глобальной сети в различных условиях. Теория массового обслуживания предоставляет нам инструментарий анализа влияния скорости передачи в глобальной сети на производительность канала связи между локальными сетями. Подобный анализ позволяет вычислить необходимую скорость работы глобальной сети, исходя из требований локальной сети пользователя.
ОЧЕРЕДЬ, АХ, ЭТА ОЧЕРЕДЬ...
Конечно, далеко не все из нас мыслят в терминах теории массового обслуживания - науки об очередях, - однако любой человек сталкивается с очередями каждый день. Выезд с маленького переулка на широкий проспект, посещение банка, покупка железнодорожного билета - вот лишь несколько примеров очередей. Если вдуматься, даже простая пересылка электронного сообщения одному из коллег тоже связана с организацией очереди.
Любая очередь включает в себя несколько составляющих. Во-первых, имеется некий входной процесс - приход клиентов, поступление больных, прибытие кадров данных. Во-вторых, каждый из поступивших объектов некоторым образом обслуживается: пассажир покупает билет в кассе, а кадр данных преобразуется из формата Ethernet в формат кадра данных протокола канального уровня в маршрутизаторе или мосте (после такого преобразования кадр данных можно передавать через глобальную сеть).
Такая система носит название одноканальной однофазной системы очередей. Она состоит из одной очереди и одного устройства обслуживания. Термин "одноканальная" говорит о том, что к устройству обслуживания ведет только один путь; термин "однофазная" означает, что обслуживание совершается в одном месте и в одну стадию. Например, двухпортовый мост, один порт которого подключен к локальной сети, а другой - к глобальной сети, представляет собой пример одноканальной однофазной системы очередей.
СДВИГ ПО ФАЗЕ
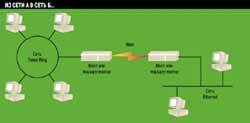
Информационная структура, где две локальные сети соединены между собой каналом связи глобальной сети, больше похожа на систему очередей другого типа, именуемого одноканальной двухфазной системой. На Рис. 1 показана схема соединения двух локальных сетей при помощи мостов или маршрутизаторов. Обратите внимание, что для передачи кадра данных от одной локальной сети к другой он должен быть обслужен двумя устройствами (в данном случае двумя мостами или двумя маршрутизаторами), поэтому такая схема может быть описана в рамках одноканальной многофазной модели. (Описание потока данных от одной локальной сети к другой в рамках одноканальной многофазной модели является математически корректным, однако так ли уж необходимо работать именно в рамках такой модели? Ответить на этот вопрос помогает анализ потока данных от одной сети к другой.)
 (1х1)
(1х1)
Рисунок 1.
Наиболее узкое место информационного потока между двумя удаленными
друг от друга локальными сетями - канал связи глобальной сети, пропускная
способность которого обычно существенно меньше скорости работы локальной
сети.
Возвращаясь к Рис. 1, представим себе, что рабочая станция сети Token Ring передает кадр данных в сеть Ethernet. Передаваемый кадр вначале "путешествует" из сегмента сети к мосту или маршрутизатору с той скоростью, на которой работает сеть (4 или 16 Мбит/с). Попав в маршрутизатор или мост, кадр копируется из сети в буфер устройства, преобразуется в другой формат, а затем (при наличии свободного канала) передается через глобальную сеть со скоростью, гораздо меньшей, чем та, с которой кадр передавался из локальной сети на устройство маршрутизации. Если непосредственно перед текущим кадром на сетевое устройство попал другой кадр, то нашему кадру придется подождать (в буфере), до тех пор пока предыдущий кадр не будет обслужен. Время обслуживания текущего кадра зависит от того, сколько кадров пришло на сетевое устройство непосредственно перед текущим: чем больше таких кадров, тем дольше время ожидания.
Рассмотрим теперь, как выполняется обслуживание кадра на противоположном конце канала глобальной сети. Поступая из глобальной сети на мост/маршрутизатор, кадр преобразуется к формату локальной сети и передается в локальную сеть. Поскольку скорость передачи информации по глобальной сети всегда ниже скоростей передачи кадров в локальной, никаких очередей при таком обслуживании не возникает, стало быть основной вклад во время обслуживания кадра на втором мосте/маршрутизаторе вносит само устройство. И это лишь малая доля от времени задержки кадров на первом мосте/маршрутизаторе. Отсюда следует, что для описания двухточечных линий связи между локальными сетями можно спокойно использовать одноканальную однофазную модель.
ПРИМЕНЕНИЕ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Используя математический аппарат теории массового обслуживания, можно вычислить зависимость времени передачи кадров от скорости работы глобальной сети без подключения к реальным каналам. Такие вычисления позволяют ответить на множество вопросов относительно производительности сети; благодаря им становится понятным, каково среднее время задержки кадров на мосте/маршрутизаторе, как может повлиять на величину этих задержек рост скорости работы канала связи глобальной сети и при каких условиях рост скорости обмена информацией по каналам глобальной сети не приводит к существенному увеличению производительности моста/маршрутизатора. Рассмотрим конкретный пример, показывающий, как теория массового обслуживания позволяет ответить на эти вопросы.
Представьте себе, что вам необходимо соединить две удаленные друг от друга локальные сети (одна из которых - Token Ring, а другая - Ethernet) при помощи двух маршрутизаторов (см. Рис. 1). Согласно оценкам, суммарный трафик между сетями составляет 16000 кадров в день, а средняя длина кадра равна 1250 байтам.
Чтобы использовать теорию массового обслуживания, необходимо знать соотношение между скоростью поступления "заказов" и скоростью обслуживания. Скорость поступления заказов может быть вычислена исходя из интенсивности трафика. Например, если обе локальные сети находятся в одном и том же часовом поясе, а продолжительность рабочего дня составляет восемь часов, то трафик интенсивностью 16000 кадров в день соответствует интенсивности поступления заказов, равной 0,556 кадров в секунду. В нашем случае скорость поступления заказов характеризует среднюю скорость поступления кадров на устройство обслуживания.
Преобразование кадров к формату глобальной сети обычно состоит в добавлении заголовка и хвостовой части к кадрам формата локальной сети. Для примера предположим, что к среднему кадру локальной сети добавляется 25 байт, в результате средняя длина кадра глобальной сети составит 1275 байт.
Для подсчета скорости обслуживания следует задаться определенным значением скорости работы глобальной сети. При этом совершенно неважно, насколько близка к оптимальной взятая в качестве начального приближения скорость обмена информацией по глобальной сети, поскольку все вычисления легко повторить для другого значения скорости. Для начала примем скорость обмена информацией равной 19200 бит/с. Тогда время, необходимое для передачи одного кадра длиной 1275 байт, составит 0,53 секунды.
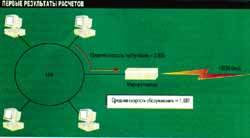
Время передачи кадра отождествляется с ожидаемым временем обслуживания. Ожидаемое время обслуживания равно 0,53 секунды, откуда получаем, что средняя скорость обслуживания (величина, обратная к ожидаемому времени обслуживания) составляет 1,887 кадров в секунду (см. Рис. 2).
 (1х1)
(1х1)
Рисунок 2.
Среднее время обслуживания зависит от средней длины кадра и скорости
работы линии.
Продолжим рассмотрение нашего примера. Если 16000 кадров за восьмичасовой рабочий день - это максимальный трафик, который можно ожидать для любого из двух направлений, то требуемая скорость работы глобальной сети рассчитывается на основе информации о трафике, передаваемом в любом из двух направлений. Поскольку в полнодуплексной линии связи скорости передачи информации в обоих направлениях равны друг другу, то нам не придется повторять расчет для передачи данных в обратном направлении. Таким образом, подсчитав скорость работы канала связи, необходимую для обработки ожидаемого максимального трафика, мы автоматически определим требуемое значение скорости передачи информации в обоих направлениях.
Если средняя скорость обслуживания превосходит среднюю скорость поступления заказов (как это имеет место в нашем случае), то никаких очередей не возникает: канал связи глобальной сети, работающий со скоростью 19200 бит/с, для нашей конфигурации более чем достаточен. Не следует, однако, забывать, что скорость поступления заказов - это средняя по времени величина. Бывает (например при передаче файлов), что рабочие станции выдают данные крупными порциями, интенсивность которых превосходит возможности маршрутизатора. Когда такое случается, маршрутизатор копирует все необходимые кадры из сети в свой буфер, где они и пребывают до тех пор, пока маршрутизатор не преобразует их в кадры глобальной сети и не передаст по глобальной сети. Теория массового обслуживания позволяет оценить задержку проходящих через маршрутизатор кадров, исходя из скорости работы линии связи; при необходимости, скорость передачи данных по линии можно изменить.
Степень использования технических возможностей обслуживающего устройства (в нашем случае степень использования маршрутизатора или моста - P) в одноканальной однофазной системе можно определить, поделив среднюю скорость поступления заказов на среднюю скорость обслуживания. В предыдущем примере P равно частному от деления 0,556 на 1,887, то есть 0,295. Таким образом, при использовании канала связи пропускной способностью 19200 бит/с средняя степень применения обслуживающего устройства составляет примерно 30%. Зная степень использования обслуживающего устройства, довольно легко определить вероятность отсутствия заказов (обслуживаемых кадров) в данный момент времени. Эта вероятность, обозначенная нами как P0, равна единице минус степень использования канала (P0 = 1 - P).
Подставляя числа, полученные для маршрутизатора, подключенного к каналу с пропускной способностью 19300 Кбит/с (P0 = 1 - 0,295 = 0,695), определяем, что вероятность отсутствия очереди кадров в маршрутизаторе составляет 69,5%.
ОБНАРУЖЕНИЕ КАДРОВ
Получив некоторые сведения относительно степени использования обслуживающего устройства, выясним теперь, каким образом кадры скапливаются в очередях и как влияют связанные с этими очередями задержки на процесс передачи кадров от одной локальной сети к другой.
В теории массового обслуживания среднее число объектов (unit) в системе обычно обозначается L, а среднее число объектов в очереди - Lq. Для одноканальной однофазной системы, L равняется средней скорости поступления заказов, деленной на разность между средней скоростью обслуживания и скоростью поступления заказов.
В нашем примере значение L дает ожидаемое число кадров, находящихся в маршрутизаторе или передаваемых по глобальной сети. Поделим скорость поступления заказов (0,556) на разность между скоростью поступления заказов и скоростью обслуживания (1,887 - 0,556). В этом случае значение L равно 0,418.
Таким образом, в буфере маршрутизатора и линии связи в любой момент находится чуть больше 40% одного кадра. Чтобы определить среднее число объектов в очереди (Lq), перемножим степень использования обслуживающего устройства (P = 0,295) на число объектов в системе (L = 0,418). Наша система обрабатывает кадры данных, поэтому длина очереди равна 0,123 кадра.
Итак, в любой момент времени в очереди маршрутизатора нашей сети (пропускная способность глобальной сети 19200 бит/с, интенсивность трафика 16000 кадров в день) находится 0,123 кадра. Чуть выше мы выяснили, что общее число кадров в системе составляет 0,418, поэтому разность этих величин (0,418 минус 0,123), равная 0,295, дает нам число кадров, передаваемых в данный момент времени по каналу глобальной сети.
РАСЧЕТ ВРЕМЕНИ
Теория массового обслуживания позволяет рассчитать среднее время нахождения объекта в системе (W) и среднее время ожидания в очереди (Wq).
Среднее время нахождения в системе представляет собой величину, обратную разнице между скоростью обслуживания и скоростью поступления заказов. Подставив числа из нашего примера, найдем, что в данном случае каждый кадр проводит в системе в среднем 0,75 секунд.
Таким образом, можно ожидать, что вызванная наличием очередей задержка кадров при передаче по линии пропускной способностью 19200 бит/с составит в среднем 0,75 секунд. Хорошо это или плохо? Все зависит от того, какого рода информацию переносят кадры. Например, если канал связи используется преимущественно для передачи электронной почты или загрузки файлов, то такая задержка будет, скорее всего, совершенно незаметна. С другой стороны, если речь идет об интерактивном обмене запросами и ответами, то задержка в три четверти секунды довольно существенна. Заметим вдобавок, что подсчитанная нами задержка кадров при передаче составляет лишь часть полного времени ответа удаленной системы. Чтобы вычислить этот параметр, надо ко времени задержки при передаче добавить время доступа к данным на удаленном компьютере и задержку, связанную с передачей ответа на запрос.
Очереди в системе можно охарактеризовать еще одним параметром, а именно временем ожидания. В нашем случае значение Wq равно произведению времени ожидания в системе на степень использования обслуживающего устройства. Таким образом, для нашей сети Wq равно 0,221 секунд.
Как было подсчитано выше, ожидаемое время нахождения кадра в системе составляет 0,75 секунд. Сюда входит время ожидания в очереди и время передачи по линиям связи. Только что мы видели, что время ожидания равно 0,221 секунд. Разность между этими значениями (0,75 минус 0,221, или примерно 0,53) дает время, затрачиваемое на передачу одного кадра по каналу глобальной сети пропускной способностью 19200 бит/с.
АВТОМАТИЗАЦИЯ ПРОЦЕССА
Далеко не каждый будет рад предложению много раз проделать одни и те же выкладки. К счастью, расчеты по теории массового обслуживания легко поддаются автоматизации. В частности, для автоматизации расчетов можно использовать электронные таблицы Lotus (см. Таблицу 1, где приведены значения восьми параметров теории массового обслуживания для 14 скоростей работы канала связи). Пользователь должен ввести значения трех переменных. В нашем случае пришлось задать число кадров в день (16000), среднюю длину кадра (1275) и продолжительность рабочего дня в часах (8).
Рассмотрим вначале колонку "Скорость линии в бит/с". Отметим, что значения 9600 и 19200 бит/с соответствуют наиболее распространенным аналоговым и цифровым арендованным линиям, в то время как скорости выше 56000 бит/с соответствуют цифровым линиям разных типов; все они представляют собой неполные каналы T-1. Поскольку часть общей пропускной способности T-1 (1,544 Мбит/с) используется для передачи служебной информации, в наших расчетах мы принимали пропускную способность этого канала равной 1536000 бит/с.
Каждая из прочих колонок по-своему интересна, однако поговорим пока только о трех из них. Содержимое двух из этих трех колонок, а именно "Степень использования канала" и "Вероятность отсутствия кадров в системе", позволит нам глубже вникнуть в суть процесса выбора оптимальной скорости работы канала. Для начала определим суммарное время ожидания: при 19200 бит/с этот параметр равен 0,75 секунд, при 64 Кбит/с - 0,17 секунд, а при 128 Кбит/с - 0,08 сек. Повышение пропускной способности глобальной сети с 19200 до 56000 бит/с приводит к снижению времени ожиданияпримерно на 0,55 секунд. С другой стороны, повышение пропускной способности с 64000 до 128000 бит/с уменьшает время ожидания всего на 0,09 секунд. В результате увеличение пропускной способности свыше 64000 бит/с приводит к незначительному выигрышу во времени ожидания.
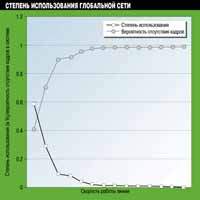
Данные, содержащиеся в колонках "Степень использования канала" и "Вероятность отсутствия кадров в системе" Таблицы 1, представлены графически на Рис. 3. Эти графики со всей очевидностью указывают на то, что по мере уменьшения степени использования канала вероятность отсутствия кадров в системе быстро растет. Хорошо видно также, что при скоростях работы канала выше 128000 бит/с степень использования канала близка к нулю, а вероятность отсутствия кадров в системе равна практически единице.
 (1x1)
(1x1)
Рисунок 3.
Закономерное уменьшение выигрыша во времени ожидания по мере роста
пропускной способности особенно хорошо видно при сравнении производительности
глобальной сети для каналов с разной пропускной способностью. При увеличении
пропускной спосбности канала связи выше пятого уровня (128000 бит/с) вероятность
отсутствия кадров в системе практически не растет.
Приведенный график иллюстрирует снижение выигрыша от установки скоростных линий с пропускной способностью выше 64000 бит/с. Подмеченная закономерность существенно упрощает выбор оптимальной пропускной способности канала глобальной сети. Ясно, что в нашем случае любой администратор сети выберет канал пропускной способностью не выше 128000 бит/с - в противном случае говорить о разумном использовании ресурсов глобальной сети не приходится. Тем не менее стоит запомнить, что теория массового обслуживания не панацея от всех бед - она просто позволяет оценить влияние пропускной способности канала глобальной сети на производительность локальной сети с учетом особенностей последней.
Гилберт Хелд - лектор и автор книг по информационным системам. Среди его последних работ - "Ethernet Networks: Design, Implementation, Operation, Management" и "Protecting LAN Resources: A Comprehensive Guide to Securing, Protecting and Rebuilding a Network" (обе эти книги вышли в издательстве John Wiley & Sons). С ним можно связаться через Internet по адресу: 235-8068@mcimail.com.
ТАБЛИЦА 1 - ВАРЬИРОВАНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ ГЛОБАЛЬНОЙ СЕТИ
|
|
|
|
|
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|