В процессе создания больших программных комплексов накапливаются версии исходных текстов программ, хранимых в различных каталогах (папках, директориях). Частой операцией при этом является определение различий между версиями файлов. Существуют программы сравнения как файлов, так и директорий. Для сопоставления версий исходных текстов программных модулей используются рекурсивные алгоритмы поиска наибольших подпоследовательностей или подстрок в символьных массивах [1]. Такие алгоритмы работают сравнительно медленно. В литературе и в Интернете превалируют программы сравнения файлов только по контрольной сумме. Однако для сопоставления версий программных модулей необходимо и достаточно сравнивать текстовые строки в целом, для чего автором предложено использовать хеширование [2] строк.
В 1998 г. была создана утилита сопоставления двух каталогов для ОС QNX. В результате ее работы, во-первых, показывалась разница в дате последней модификации каждого отличающегося модуля, а во-вторых (и это самое важное), — все различия в текстах версий модулей. При этом быстродействие множественного сравнения всех текстовых файлов каталогов оказалось выше по сравнению со стандартными утилитами QNX.
Рассмотрим подробно задачу сравнения двух текстовых файлов.
Для сравнения файлов необходимо сопоставлять их строки, представляющие собой последовательности восьмибитовых символов. Если пару строк сравнивать посимвольно, то на сопоставление всех строк двух файлов понадобится слишком много времени. Вместо этого автором предложено арифметическое кодирование строк числами с плавающей запятой.
Суть арифметического кодирования состоит в том, что каждая i-я строка заменяется числом с плавающей запятой по следующему алгоритму.
- Установить порядковый номер j-го символа в строке i равным нулю (начальный символ в строке считаем нулевым по порядку). Установить k = 0,0 - арифметический код строки.
- Получить степенной множитель e вида e = Ej, где Е = 1,1111111.
- Выполнить k = k+Сje, где Cj - код j-го символа строки.
- Если j не является номером последнего символа строки, то
j = j+1 и повторить с шага 2.
Иначе - шаг 5. - Присвоить элементу m[i] массива кодов строк файла значение m[i] = k.
Конец кодирования строки файла.
Оригинальным в этом алгоритме является выбор для арифметического кодирования основания степени с плавающей точкой — числа Е, значение которого (Е = 1,1111111) незначительно отличается от единицы. При этом не появляется ограничения на максимальную величину кода строки, т.е. на максимальное число символов в строке.
Теперь вместо двух символьных файлов мы имеем два числовых массива m1 и m2, размер которых определен числом строк в исходных файлах.
Остается сопоставить два этих массива. Массив m1 будем считать исходным, а массив m2 — измененным. Теперь следует выявить удаленные из исходного массива строки, добавленные к нему строки и измененные в исходном массиве строки. Для этого автором предложен автоматный алгоритм (построение фрагмента которого представлено в [3]), граф переходов автомата показан на схеме.
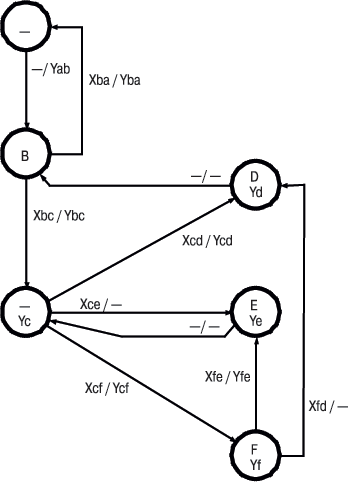
|
| Рис. 1. Граф переходов автомата |
Кратко смысл данного алгоритма состоит в следующем.
Поочередно сравниваются два элемента массивов до тех пор, пока они не станут различными. Затем номер элемента нового массива увеличивается на единицу и перебор элементов исходного массива продолжается (начиная с номера элемента, следующего за теми, которые не совпали) до появления равных элементов (найдено различие) или до конца массива, после чего вновь увеличивается на единицу номер второго массива. Когда найдено различие, по последним номерам элементов массивов делается вывод: если последний номер элемента исходного массива на единицу больше номера последней совпавшей пары, то налицо вставка; если последний номер элемента нового массива на единицу больше номера последней совпавшей пары, то налицо удаление; в противном случае имеет место замена группы строк новой группой строк.
Подробный алгоритм. Используем следующие обозначения:
cycle - признак продолжения цикла автоматного алгоритма,
b1, b2 - номера элементов двух массивов,
c1, c2 - то же,
g1, g2 - верхние границы изменения номеров строк,
f1, f2 - номера строк для поиска повторов,
v1, v2 - запоминаемые номера последней сравнивавшейся пары строк,
Хab - условие перехода из вершины (состояния) A в вершину (состояние) B,
Yab - действие на переходе из вершины A в вершину B,
Ya - действие в состоянии (вершине) А.
Рассмотрим состояния и переходы автомата.
Состояние (вершина) А: исходное.
Из состояния А при входе в программу осуществляется безусловный переход в состояние В с выполнением действия Yab на переходе:
Yab: b1 = b2 = -1 — подготовка к перебору элементов двух сравниваемых массивов.
Состояние В: ожидание неодинаковых элементов массивов или конца массивов.
Возврат в состояние А при условии
Xba = (m1==NULL || m1[0]==0.0 (исходный массив не определен или имеет нулевую длину) ||
m2==NULL || m2[0]==0.0 (новый массив не определен или имеет нулевую длину) ||
m1[b1] == m2[b2] && m1[b1]==0.0) (достигнут конец обоих массивов).
Действие на переходе из В в А:
Yba: cycle = 0 — конец цикла обработки, конец алгоритма.
Переход из состояния В в состояние С при условии
Xbc = (m1[b1] != m2[b2]) — достигнуты неравные элементы массивов, что является признаком удаления, вставки или замены.
Действия на этом переходе:
Ybc: 1) c1 = b1;
2) c2 = b2 - запоминаем номера несравнивавшихся элементов массивов;
3) g1 = g2 = MAXSTR - установить максимальное значение числа сравниваемых элементов;
4) v1 = v2 = 0.
Состояние С: ожидание одинаковых элементов массивов после удаления, вставки, замены. Действие в этом состоянии:
Yc: if(m2[b2]>0.0 || m2[c2]>0.0) ++c2 — если элемент нового массива не последний, то переход к очередному элементу нового массива.
Переход из состояния С в состояние F при условии
Xcf = (m1[c1] == m2[c2]) — конец вставки, удаления или замены.
Действия на этом переходе:
Ycf: 1) f1 = v1 = c1; 2) f2 = v2 = c2 — запоминание текущих номеров элементов массивов.
Переход из состояния С в состояние Е при условии
Xce = (m2[c2]==0.0 && m1[c1]>0.0 || (c2 == g2) && c1 < g1-1) — конец второго массива или достигнута граница просмотра массивов.
Переход из состояния С в состояние D при условии
Xcd = (c1 == g1-1 && c2 == g2) — достигнуты границы просмотра массивов.
Действия на этом переходе:
Ycd: 1) c1 = v1; 2) c2 = v2 — восстановление запомненных номеров элементов массивов.
Состояние D: действия в нем Yd: печать вставки, удаленной порции строк, замененной порции строк:
Yd: 1) если (c1 == b1 && c2 > b2) - вставка, то печать строк b2 (c2-1 из второго файла как вставленных;
2) если (c2 == b2 && c1 > b1) - удаление, то печать строк b1 ( c1-1 из первого файла как удаленных;
3) если (c1 > b1 && c2 > b2) - замена, то печать строк b1 (c1-1 из первого файла как удаленных и печать строк b2 ( c2-1 из второго файла как вставленных;
4) b1 = c1 - 1 5) b2 = c2-1 - подготовка к продолжению сравнения массивов.
Состояние Е: модификация номера элемента исходного массива:
Ye: если (c1 < g1-1) - не достигнута граница перебора номеров элементов исходного массива, то 1) c1 = с1+1;
2) c2 = b2-1 - второй массив просматривается с позиции, в которой были найдены различные элементы.
Состояние F: поиск еще одного точно такого же элемента в первом массиве:
Yf: если (m1[f1]>0.0 && f1 < g1-1) — не конец границы поиска, то
f1 = f1 + 1.
Переход из состояния F в состояние D:
Xfd = (m1[f1]==0.0 || f1 == g1-1) — достигнута граница перебора.
Переход из состояния F в состояние E:
Xfe = (m1[f1] == m2[f2]) — найден повтор того же элемента в исходном массиве.
Yfe: 1) g1 = f1 — установка границы для первого массива;
2) g2 = c2.
Конец описания алгоритма.
Представленные алгоритмы были запрограммированы в ОС QNX как утилита сравнения двух каталогов и выявления различий в парных файлах каталогов. Эксплуатация этой программы продолжалась несколько лет, и сбоев из-за ошибок в ее работе не замечено. Программа была настроена на текстовые файлы с расширениями: .c, .cpp, .h, .hpp.
В принципе алгоритм пригоден для произвольных текстовых файлов в кодировке ASCII, но его можно распространить и на другие форматы, например WORD, если задаться определенным признаком конца строки или конца предложения. Размер строк практически неограничен.
Литература
- Кнут Д. Искусство программирования для ЭВМ. Т. 3: Сортировка и поиск. М.: Мир, 1978. 844 с.
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.: МЦМНО, 1999. 960 с.
- Кузнецов Б.П. Психология автоматного программирования // BYTE/Россия. 2000. №11. С. 22-29.
Об авторе
Борис Павлович Кузнецов — докт. техн. наук, декан факультета компьютерных наук (информатики) Международного университета фундаментального обучения (МУФО, Санкт-Петербург).
